- #1
pingpong240
- 27
- 0
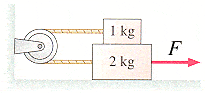
The lower block in Figure P8.28 is pulled on by a rope with a tension force of F = 28 N. The coefficient of kinetic friction between the lower block and the surface is 0.40. The coefficient of kinetic friction between the lower block and the upper block is also 0.40. What is the acceleration of the 2.0 kg block?
 Relevant Equations
Relevant Equations
f_k = uN
Newton's 2nd and 3rd Laws
What I Did
Well I made two systems, one with the block on the bottom (block 1) and one with the block on the top (block 2). Now one thing that seemed confusing to me was that block 1 was being pulled with a force of 28 N, but in the picture the force is depicted going away from the wall. I'm not too sure where block 2 comes into play, other than enacting a frictional force on block 1. So this is how I have Newton's 2nd law set up:
Force_1x = friction(2 on 1) + friction (floor on 1) - 28 N
= .4 (1) + .4(2) - 28 N
Force_1y = 0
Force_2x = 28 N - friction(1 on 2)
= 28 N - .4(2)
Force_2y = 0
But this gets me a somewhat high acceleration, that is not right.
As you can see, I'm doing something seriously wrong here. Please help me with this problem!
f_k = uN
Newton's 2nd and 3rd Laws
What I Did
Well I made two systems, one with the block on the bottom (block 1) and one with the block on the top (block 2). Now one thing that seemed confusing to me was that block 1 was being pulled with a force of 28 N, but in the picture the force is depicted going away from the wall. I'm not too sure where block 2 comes into play, other than enacting a frictional force on block 1. So this is how I have Newton's 2nd law set up:
Force_1x = friction(2 on 1) + friction (floor on 1) - 28 N
= .4 (1) + .4(2) - 28 N
Force_1y = 0
Force_2x = 28 N - friction(1 on 2)
= 28 N - .4(2)
Force_2y = 0
But this gets me a somewhat high acceleration, that is not right.
As you can see, I'm doing something seriously wrong here. Please help me with this problem!