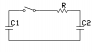
- #1
Clever-Name
- 380
- 1
Homework Statement
In the circuit show below, C1 = 5 microfarads, C2 = 10 microfarads and R = 1000 ohms. Initially, the switch is open, C1 is charged to 20 volts, and C2 is uncharged. At time t=0 the switch is closed.
(a) Calculate the voltage across C1 at a much later time. Hint: consider charge conservation.
(b) The energy stored in a charged capacitor is given by U = CV2/2. Calculate the energy stored in C1 and C2 before and after closing the switch.
(c) Derive an expression for the power dissipated in R as a function of time for t>0.
(d) Integrate your expression from (c) to find the total energy dissipated by R. Compare with your answer from (b).
*see attachment for image of circuit*
Homework Equations
[itex] \frac{1}{C_{eq}} = \frac{1}{C_{1}} + \frac{1}{C_2}[/itex]
[itex] U = \frac{1}{2}CV^{2} [/itex]
[itex] P = I^{2}R [/itex]
[itex] Q = CV[/itex]
The Attempt at a Solution
a) [itex] Q = C_{1}V = 100{\mu}F [/itex]
I initially tried adding the capacitances in series but wound up with 30V as my answer, so i figured that must be wrong (how can the voltage go up? :S) So then I did this:
[itex] V = \frac{Q}{C_{1} + C_{2}} = \frac{100{\mu}F}{15{\mu}F} = 6.67V[/itex]
That's 6.67 V across both capacitors, therefore 6.67 across C1
b) Assuming my answer from a is right:
[itex] U_{1}_{i} = \frac{1}{2}CV^{2} = 0.001 J [/itex]
[itex] U_{1}_{f} = 1.11 {\times} 10^{-4} J [/itex]
[itex]U_{2}_{i} = 0[/itex]
[itex]U_{2}_f} = 2.22 {\times} 10^{-4} J[/itex]
c) Here's where I get confused, I honestly have no clue where to start. I've never dealt with a circuit like this before, so I don't know how to set up KVL or KCL to solve for a time-varying current or voltage.
Help please!