- #1
Firepanda
- 430
- 0
I need to calculate the norm of the ideal
p = (3, 1 - √-5)
All the information I have is that it's a prime ideal.
I managed to calculate the normal of the ideal q = (3, 1 + √-5) (which was 3) by finding a the determinant of a base change matrix by considering an integral basis
Here I'm not sure how to do that (in the other example I managed to show an equivelence relation so that I could find an integral bases)
Here is a similar example with the ideal p1 = (2, 1 + √-17)
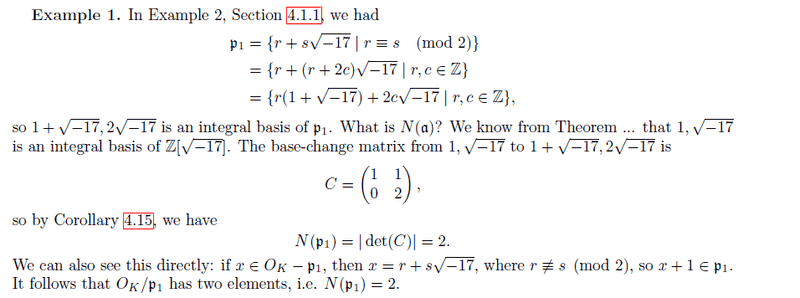
Any help appreciated, thanks.
p = (3, 1 - √-5)
All the information I have is that it's a prime ideal.
I managed to calculate the normal of the ideal q = (3, 1 + √-5) (which was 3) by finding a the determinant of a base change matrix by considering an integral basis
Here I'm not sure how to do that (in the other example I managed to show an equivelence relation so that I could find an integral bases)
Here is a similar example with the ideal p1 = (2, 1 + √-17)
Any help appreciated, thanks.