- #1
phy5ic5
- 8
- 0
Homework Statement
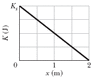
A block is sent up a frictionless ramp along which an x-axis extends upward. The figure below gives the kinetic energy of the block as a function of position x; the scale of the figure's vertical axis is set by Ks = 46.0 J. If the block's initial speed is 4.50 m/s, what is the normal force on the block?
Homework Equations
Fn=mg
K=(1/2)m(v^2)
The Attempt at a Solution
Solved K=(1/2)m(v^2) for m and got 4.54 kg.
Plugged m into Fn=mg.
I got 44.5 N but this is not correct. What am I doing wrong?
Attachments
Last edited: