Normalised 2D coordinates on a surface

[mat_davies]

Homework Statement

I'm trying to find normalised 2D coordinates for a point (Px,Py,Pz) that lies on a planar surface, which is defined by straight lines between 4 points c1-c4 (numbered anticlockwise).

Homework Equations

General vector equations

The Attempt at a Solution

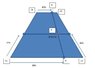
Suppose the point c1 is in the bottom left corner. The horizontal lines bounding the top and bottom of the surface are i) from c1 to c2 and ii) from c4 to c3. A normalised x-coordinate creates a pair of points (M,N) that are an equal proportion along both lines. M and N are chosen such that a a line from M to N passes through P. A similar y-coordinate is used to locate the point vertically.

The diagram below shows an example, with (normally unknown) normalised coordinates (0.8,0.5)

to find the normalised coordinates:

Suppose A is the normalised x-coordinate

Mx=A(c2x-c1x)
My=A(c2y-c1y)
Mz=A(c2z-c1z)
Nx=A(c3x-c4x)
Ny=A(c3y-c4y)
Nz=A(c3z-c4z)

A line from M to N must have the same unit vector as a line from M to P

(Nx-Mx)/((Nx-Mx)^2+(Ny-My)^2+(Nz-Mz)^2)^.5)=(Px-Mx)/((Px-Mx)^2+(Py-My)^2+(Pz-Mz)^2)^.5)

and similar for (Ny-My) and (Nz-Mz)

I now have the following problem

i) The equation above does not seem to be able to generate a closed form expression for A
ii) A appears to cancel in the LHS of the equation above (given that 0<A<1, so it can be taken out of the square root). This suggests that the unit vector is independent of the normalised x-coordinate, which doesn't seem to be correct.

Can anybody help with this? or think of a better method?

Cheers

Mat

 

[anathema]

Dear Mat,

Thank you for your question. It seems that you have a good understanding of the problem and have made a good attempt at finding a solution. However, I believe there may be a simpler approach to finding the normalised coordinates for a point on a planar surface defined by four points.

First, let's define the four points as c1, c2, c3, and c4, with c1 being the bottom left corner and the points numbered counterclockwise.

To find the normalised x-coordinate, we can first find the distance between c1 and c2, and then the distance between c1 and the point P. This will give us the proportion of the distance along the line from c1 to c2 that P is located. We can then use this proportion to find the x-coordinate of P along the line from c1 to c2.

Using the Pythagorean theorem, we can find the distance between c1 and c2 as:

d1 = √[(c2x - c1x)^2 + (c2y - c1y)^2 + (c2z - c1z)^2]

Similarly, the distance between c1 and P can be found as:

d2 = √[(Px - c1x)^2 + (Py - c1y)^2 + (Pz - c1z)^2]

Now, we can find the normalised x-coordinate, A, as:

A = d2/d1

Similarly, we can find the normalised y-coordinate, B, by finding the distance between c1 and c4, and then the distance between c1 and P, and using the same formula as above:

d3 = √[(c4x - c1x)^2 + (c4y - c1y)^2 + (c4z - c1z)^2]

d4 = √[(Px - c1x)^2 + (Py - c1y)^2 + (Pz - c1z)^2]

B = d4/d3

Therefore, the normalised coordinates for point P would be (A, B).

I hope this helps and provides a simpler solution to your problem. Let me know if you have any further questions or if you need clarification on anything.