- #1
mubashirmansoor
- 260
- 0
Hello, About sometime ago, I came up with the following results, which might seem useless but it is very interesting from my point of view,
I'd be glad to have your comments,
Thankyou.
______________________________________________________________
I’ve found that there are possibilities for writing formulas for polynomial sequences which are independent of the law or the equation ruling the them & I was successful in writing the formulae, with its specific range which depends on the differentiated function’s equation or in other words the rate of changes between the terms. The method used is mainly following a numerical triangle which is due to the laws of calculus, in order to write the formula I had to propose the ‘M’ theorem too, which states that all types of series have the number “m” which is the key for finding the next term, (read *logic behind M theory* p.2)
For better understanding about the value “m” let’s take an example,
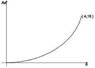
The sequence: 1, 8, 27, 64, 125… which follows an equation ( n^3 )
The following chart should be plotted, (see dig1, attached)
In this example the number “6” is reoccurring and if we keep on writing the next terms of the sequence we will again end up with the number “6”, which I called it “m”.
The theory then states that the letter m + 24 + 61+125 = 216 = 6^3 = 6th term.
By using the same method we can write an algebraic expression for the letter “m” and the 5th or 6th terms, in the following way;
5th term = v 4th term = w 3rd term = z 2nd term = y 1st term = x
Hence m = [ ( w – z ) – ( z – y ) ] – [ ( z – y ) – ( y –x ) ]
m = w – 3z + 3y – x
& the expression for the 5th term will be ;
v = m + [ ( w – z ) – (z – y ) ] + ( w – z ) + w
v = 4w – 6z + 4y – x
Now by inserting any of the four consecutive terms of the sequence we can get the fifth but this formulae involves a range where the second derivative of the function should be zero or linear other wise the formula is not applicable. To improve the range we shall add the number of consecutive terms inserted in the formulae. But still there must be a way to improve the range without adding the variables where I have not yet been successful in finding the method…
By using the same technique I have derived the formulae for the 6th term of a sequence by inserting any 5 consecutive terms; u = 6th term.
u = 5v – 10w + 10z – 5y + x
With a range, where the 3rd derivative of the function should be either linear or zero.
After some observations we can conclude that the formulas for different terms are actually following the rule given below;
nth term = (n – 1) C ( 1 ) (f(n-1)) – (n-1)C( 2 ) (f(n-2)) + ……………….. + (n-1) C (n-1) (f(1))
To indicate which parts of the formulae should be negative or positive you have to use the following method,
When “ r ” is even that specific part of the formula should be negative and if “ r “ is odd vice versa.
As an example to write the formulae for “u” (the 6th term) using the law given above;
u = (6-1) C 1(v) – 5 C 2(w) + 5 C 3(z) – 5 C 4(y) + 5 C 5(x)
u = 5v – 10w + 10z -5y + x which means
f(6) = 5f(5) – 10f(4) + 10f(3) – 5f(2) + f(1)
By using the same formulae we can even get the nth term of the sequence as given below:
First evaluate the 6th term and substitute the 6th term’s value in v (the fifth term) in other words use the terms; 2nd, 3rd, 4th, 5th & 6th to get the seventh and so on. We can do this because it doesn’t matters that the terms inserted are the first ones the important point is that we need consecutive terms.
By following this technique we find that;
f(6) = 5f(5) – 10f(4) + 10f(3) – 5f(2) + f(1)
f(7) = 15f(5) – 40f(4) + 45f(3) – 24f(2) + 5f(5)
f(8) = 35f(5) – 105f(4) + 126f(3) – 70f(2) + 15f(1)
We can see that the factors of f(5),f(4),f(3)… are all connected to each and other by the equations which are
Factors of f(5): 5n^2 – 55n + 155
Factors of f(4): 17.5n^2 – 197.5n + 565
Factors of f(3): 23n^2 – 264n + 766
Factors of f(2): 13.5n^2 – 156.5n + 458
Factors of f(1): 3n^2 – 35n+ 103
Hence the final equation involving the variable ‘n’ is as follows;
An = (5n^2–55n+155)f(5)-(17.5n^2–197.5n+565)f(4)+(23n^2–264n+766)f(3)-(13.5n^2–156.5n+458)f(2)+(3n^2–35n+103)f(1)
Where ‘n’ is an Integer, In order to make n a real number we have to enter the terms with small delta x between them…
**The Logic behind M theory;
We can simply prove the theory using a little bit of calculus;
Take An = n2 (see dig2, attached)
By plotting the other points and connecting each consecutive point to the other by a straight line we can have their gradients so that we can then draw the graph for ‘d An / dn’ While we don’t mean the derivatives of the equation but the rate of change of terms.
Now we can draw the graphs of ‘d An / dn’ & ‘d2An / dn2’ ;
(see dig3)
As shown above graph of ‘d An / dn’ is increasing with a constant rate of 2 units/n (shown in the graph
d2n / dn2) so when n is 5 the graph ‘d An / dn’ will increase by 2 units/n (d an / dn axis will show 9), hence when n is 5 ‘An’ should be increased by 9 which means 9 + 16 = 25 = 52 = 5th term.
When it comes to the numerical triangle, we are doing the same process done by calculus because when we are subtracting the two consecutive terms in the chart given on the first page, we are actually finding the gradient as given below;
(see dig4)
As a result; 0 + 2 + 7 + 16 = 25 = 5th term.
I'd be glad to have your comments,
Thankyou.
______________________________________________________________
I’ve found that there are possibilities for writing formulas for polynomial sequences which are independent of the law or the equation ruling the them & I was successful in writing the formulae, with its specific range which depends on the differentiated function’s equation or in other words the rate of changes between the terms. The method used is mainly following a numerical triangle which is due to the laws of calculus, in order to write the formula I had to propose the ‘M’ theorem too, which states that all types of series have the number “m” which is the key for finding the next term, (read *logic behind M theory* p.2)
For better understanding about the value “m” let’s take an example,
The sequence: 1, 8, 27, 64, 125… which follows an equation ( n^3 )
The following chart should be plotted, (see dig1, attached)
In this example the number “6” is reoccurring and if we keep on writing the next terms of the sequence we will again end up with the number “6”, which I called it “m”.
The theory then states that the letter m + 24 + 61+125 = 216 = 6^3 = 6th term.
By using the same method we can write an algebraic expression for the letter “m” and the 5th or 6th terms, in the following way;
5th term = v 4th term = w 3rd term = z 2nd term = y 1st term = x
Hence m = [ ( w – z ) – ( z – y ) ] – [ ( z – y ) – ( y –x ) ]
m = w – 3z + 3y – x
& the expression for the 5th term will be ;
v = m + [ ( w – z ) – (z – y ) ] + ( w – z ) + w
v = 4w – 6z + 4y – x
Now by inserting any of the four consecutive terms of the sequence we can get the fifth but this formulae involves a range where the second derivative of the function should be zero or linear other wise the formula is not applicable. To improve the range we shall add the number of consecutive terms inserted in the formulae. But still there must be a way to improve the range without adding the variables where I have not yet been successful in finding the method…
By using the same technique I have derived the formulae for the 6th term of a sequence by inserting any 5 consecutive terms; u = 6th term.
u = 5v – 10w + 10z – 5y + x
With a range, where the 3rd derivative of the function should be either linear or zero.
After some observations we can conclude that the formulas for different terms are actually following the rule given below;
nth term = (n – 1) C ( 1 ) (f(n-1)) – (n-1)C( 2 ) (f(n-2)) + ……………….. + (n-1) C (n-1) (f(1))
To indicate which parts of the formulae should be negative or positive you have to use the following method,
When “ r ” is even that specific part of the formula should be negative and if “ r “ is odd vice versa.
As an example to write the formulae for “u” (the 6th term) using the law given above;
u = (6-1) C 1(v) – 5 C 2(w) + 5 C 3(z) – 5 C 4(y) + 5 C 5(x)
u = 5v – 10w + 10z -5y + x which means
f(6) = 5f(5) – 10f(4) + 10f(3) – 5f(2) + f(1)
By using the same formulae we can even get the nth term of the sequence as given below:
First evaluate the 6th term and substitute the 6th term’s value in v (the fifth term) in other words use the terms; 2nd, 3rd, 4th, 5th & 6th to get the seventh and so on. We can do this because it doesn’t matters that the terms inserted are the first ones the important point is that we need consecutive terms.
By following this technique we find that;
f(6) = 5f(5) – 10f(4) + 10f(3) – 5f(2) + f(1)
f(7) = 15f(5) – 40f(4) + 45f(3) – 24f(2) + 5f(5)
f(8) = 35f(5) – 105f(4) + 126f(3) – 70f(2) + 15f(1)
We can see that the factors of f(5),f(4),f(3)… are all connected to each and other by the equations which are
Factors of f(5): 5n^2 – 55n + 155
Factors of f(4): 17.5n^2 – 197.5n + 565
Factors of f(3): 23n^2 – 264n + 766
Factors of f(2): 13.5n^2 – 156.5n + 458
Factors of f(1): 3n^2 – 35n+ 103
Hence the final equation involving the variable ‘n’ is as follows;
An = (5n^2–55n+155)f(5)-(17.5n^2–197.5n+565)f(4)+(23n^2–264n+766)f(3)-(13.5n^2–156.5n+458)f(2)+(3n^2–35n+103)f(1)
Where ‘n’ is an Integer, In order to make n a real number we have to enter the terms with small delta x between them…
**The Logic behind M theory;
We can simply prove the theory using a little bit of calculus;
Take An = n2 (see dig2, attached)
By plotting the other points and connecting each consecutive point to the other by a straight line we can have their gradients so that we can then draw the graph for ‘d An / dn’ While we don’t mean the derivatives of the equation but the rate of change of terms.
Now we can draw the graphs of ‘d An / dn’ & ‘d2An / dn2’ ;
(see dig3)
As shown above graph of ‘d An / dn’ is increasing with a constant rate of 2 units/n (shown in the graph
d2n / dn2) so when n is 5 the graph ‘d An / dn’ will increase by 2 units/n (d an / dn axis will show 9), hence when n is 5 ‘An’ should be increased by 9 which means 9 + 16 = 25 = 52 = 5th term.
When it comes to the numerical triangle, we are doing the same process done by calculus because when we are subtracting the two consecutive terms in the chart given on the first page, we are actually finding the gradient as given below;
(see dig4)
As a result; 0 + 2 + 7 + 16 = 25 = 5th term.
Attachments
Last edited: