- #1
GreenCarrots
- 1
- 0
Homework Statement
The slippage of flexible belts over shafts or pulleys of circular cross sections is an important consideration in many mechanical devices. When the frictional contact between the belt and the shaft is about to be broken (that is when the slippage is imminent), a belt drive is acting under the most demanding conditions. The belt tension is not constant along the contact region. Rather it increases along the contact region between the shaft in the direction of impending slippage.
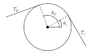
A picture is given in which a cross section of a single pulley is shown with a belt with tension T1 on one point of contact and T2 on the other, with θ1 being the point of contact from the direction T1 and θ2 being the point of contact from the direction of T2. (attached)
When slippage is imminent, the tension in the belt can be found to satisfy the differential equation dT(θ)/dθ = μT(θ)
In the figure I mentioned with the single pulley, the value of T2 can be determined by computing the solution to the following ODE in the interval θ1≤θ≤θ2:
-above equation, and T(θ1) = T1
In the figure below, calculate the tension, T, assuming that μ = .2
Homework Equations
dT(θ)/dθ = μT(θ)
T(θ1) = T1
The Attempt at a Solution
I'm not too sure how to start this, I assume I'm looking for the maximum tension before slippage occurs, right?
I tried drawing some triangles to help me find theta values. I got a little confused here though, since the point of contact with the belt intersects the side of a triangle I drew. In addition, I haven't done geometry in a while, so I don't know if I can find the proper angle values given an angle, side and side. I also know that the belt is tangent to the pulley at the point of contact.
How should I approach this problem? How do I find values for θ1?
I already figured out that T(θ) = C*e^(.2θ)
Thanks.