- #1
fitz_calc
- 41
- 0
This is an example I found online. I know how to get to this:
fitz_calc said:
This is an example I found online. I know how to get to this:, but why is 3-4x brought into the problem? sorry for the newbie questions tonight but my notes from class don't really cover the material very well, thanks.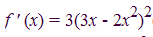
rocophysics said:that's a great way Casey, makes a lot of sense too; exactly how i learned logs
fitz_calc said:ok i think I'm getting it. i tried a homework problem:
y=(4+x^4)^5 => u=g(x)=4+x^4 , f(u)=u^5
then f(x)=f(g(x)) => 5u^4 * (4x^3) => 5(4+x^4)^4 * (4x^3)
* a bit of confusion here -- why can't I multiply the 5 by (4+x^4)^4?
I know the answer is 20x^3 (4+x^4)^4 but can't figure out why the 5 isn't distributed in the last step, thanks
A derivative is a mathematical concept that represents the rate of change of a function at a given point. It is essentially the slope of a curve at a specific point.
A derivative can be calculated using calculus methods, specifically the limit definition of a derivative. This involves finding the slope of a curve at a point by taking the limit as the distance between two points on the curve approaches zero.
Finding higher-order derivatives, also known as taking the second, third, or nth derivative, can help us understand the curvature and behavior of a function at a given point. It can also be used to solve more complex problems in physics, engineering, and other sciences.
Yes, derivatives can be negative. A negative derivative indicates that the function is decreasing at that point, while a positive derivative indicates that the function is increasing at that point.
Derivatives have many applications in real life, including physics, engineering, economics, and statistics. They are used to model and understand the rates of change, such as velocity, acceleration, and growth rates. They are also used in optimization problems to find maximum or minimum values of a function.