- #1
IgniteFlare
- 2
- 0
Hello,
I am having a little trouble understanding what the question is asking so I was hoping someone would be able to clear up the language the textbook uses. Thanks!
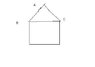
A piece of window framing material is 6m long. A carpenter wants to build a frame for a rural gothic style window where triange ABC is equilateral. The window must fit inside a space 1m wide and 3m high.
a. Find the dimensions that should be used for the 6 pieces so that the maximum amount of light will be admitted. Assume no waste of material for corner cuts, etc.
What I've done so far:
I am assuming that the window width is smaller than the length of BC.
The window framing material totals to 36m.
Thanks for the help!
I am having a little trouble understanding what the question is asking so I was hoping someone would be able to clear up the language the textbook uses. Thanks!
A piece of window framing material is 6m long. A carpenter wants to build a frame for a rural gothic style window where triange ABC is equilateral. The window must fit inside a space 1m wide and 3m high.
a. Find the dimensions that should be used for the 6 pieces so that the maximum amount of light will be admitted. Assume no waste of material for corner cuts, etc.
What I've done so far:
I am assuming that the window width is smaller than the length of BC.
The window framing material totals to 36m.
Thanks for the help!