Optimal Velocity for Projectile Path over a Sloped Roof

[timetraveller123]

Homework Statement

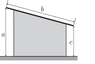
What is the minimum initial velocity that has to be given to a stone in order to throw it across a sloped roof? The roof has width b, its two edges have heights a and c.

Homework Equations

The Attempt at a Solution

i decided to start simpler so

so i first looked at if was just a wall of a
then minimal velocity would be $\sqrt{2gh}$ with a little bit of forward velocity to get it over

if it was roof like this but both sides being height a and width b then the maximum height would have to occur somewhere over the middle of roof and the trajectory would have to touch the corners

i was doing something like this but i believe it should be simpler
$v cos \theta t = x\\ v sin \theta t - \frac{g t^2}{2} = y \\ a = y\\ a = v sin \theta t - \frac{g t^2}{2} \\$
the difference between the two times of this is
$t_1 - t_2 = \frac{2}{g}\sqrt{v^2 sin\theta - a^2}\\ v cos\theta (t_1 - t_2) = b \\ v cos\theta \frac{2}{g}\sqrt{v^2 sin\theta - a^2} = b \\$
i was hoping to express v as function theta from here and minimise with respect to theta but it seems overly complicated is there any other easier method

 

[BvU]

Hello vishnu,

the difference between the two times of this is

What are you saying here ? What is $t_1$ and what is $t_2$ ? (I might guess them from:)

$$v cos\theta (t_1 - t_2) = b $$

left side is a horizontal distance, right-hand side is not (e.g. imagine c = 0)

Other than that, I think you indeed have to find a theta for which v is minimum, so the method looks good.

 

[PeroK]

if you imagine firing the projectile from the left. It must clear two instructions. That should give you some equations to work with.

 

[timetraveller123]

left side is a horizontal distance, right-hand side is not (e.g. imagine c = 0)

there is no c in my question i am asking a simpler question instead of a sloping roof imagine a non sloping roof of height a and width b the time t1 and t2 is the time for projectile to reach each of the corners

if you imagine firing the projectile from the left. It must clear two instructions. That should give you some equations to work with.

i already have an equation for $V^2(\theta)$ but it is quadratic is there a simpler solution and first i am working on my simplified problem not the actual one

 

[BvU]

Right, sorry for sloppy reading...

Not as bad as you think:
your $t_1 - t_2 = \frac{2}{g}\sqrt{v^2 \sin^2\theta - a^2}$ is dimensionally wrong, and besides: it should have the sine squared too.

tip: use ## \sin\phi ## to get $\sin\phi$ instead of ## sin\phi ## ( $sin\phi$ )

For your simple case you could try to parametrize a parabola as $y = c_1 x^2 + c_2$ and require that the points $(\pm {b\over 2} , a)$ are on it.

 

[haruspex]

The simplest approach is to consider how the speed of launch compares with the speed when skimming, say, the higher of the two corners. How does minimising that speed relate to minimising the launch speed?

 

[PeroK]

i was hoping to express v as function theta from here and minimise with respect to theta but it seems overly complicated is there any other easier method

You are correct that for the minimum speed the projectile must just clear each side of the roof.

Note that you do not want to minimise $v$ with respect to $\theta$, as you are free to fire the projectile from any distance from the building. If we let this distance be $d$, then the formulaic way to approach the problem is:

You have two equations (one for each side of the roof) for the three variables: $v$, $\theta$ and $d$. You need to eliminate $\theta$ to give $v$ as a function of $d$. Now, the task is to minimise $v$ with respect to $d$.

This is a fairly simple method, but especially where the two sides of the roof are different heights, it will get algebraically quite messy.

So, you may want to look for a further insight that simplifies the problem. Your idea to take both sides of the roof as the same height was a good one. What about also thinking about the problem from the point of view of someone standing on the flat roof in this case?

 

[BvU]

Note that you do not want to minimise vvv with respect to $theta$

We don't fully agree, since we addded 'skims a corner of the building' as a condition -- that makes $d$ and $\theta$ equivalent ...

the point of view of someone standing on the flat roof

same thing as 'skimming that corner', but conceptually nice.

 

[PeroK]

We don't fully agree, since we addded 'skims a corner of the building' as a condition -- that makes $d$ and $\theta$ equivalent ...

same thing as 'skimming that corner', but conceptually nice.

Yes, you're right. You could get $v$ as a function of $\theta$. It seemed logical to add the variable distance, but maybe that isn't the best idea!

I had a different idea in mind for the person on the roof.

 

[timetraveller123]

thanks for the wonderful replies

For your simple case you could try to parametrize a parabola as y=c1x2+c2y=c1x2+c2y = c_1 x^2 + c_2 and require that the points (±b2,a)(±b2,a)(\pm {b\over 2} , a) are on it.

i know i could do it that way but i am trying to go for a more geometric way

The simplest approach is to consider how the speed of launch compares with the speed when skimming, say, the higher of the two corners. How does minimising that speed relate to minimising the launch speed?

actually i am not considering this problem first i am considering the simpler problem i posed in post #1 i was thinking since the maximum height occurs at midway between 2 corners for the flat roof then for the sloping roof the maximum height would be more skewed towards the taller corner and for zero width wall the maximum height would occur directly above so i was thinking this can give some geometric thing as the skew maybe a trig function

actually the idea i was having was using the fact the range that projectile can be hit from the focus of parabola is given by parabola :
$y =< \frac{v^2}{2g} - \frac{g x^2}{2 v^2}$
the optimum trajectory is such that the velocity at target is tangent to the parabola at the point
i was hoping to somehow to use these two principles
but i am not sure of what exactly is the target here

so something like this

where the black curve is the range of projectile for given launching speed
and red curve is the actual trajectory i am guessing it is the right corner that is target here
but once again there is also the distance of firing from the wall to consider

 

[BvU]

You will need three equations because there are three things to be determined: firing position, speed and angle. Two equations come from skimming the corners and the other from the minimum speed requirement.

Consider it a math problem, not a physics problem. For a parabola you need three parameters.

 

[PeroK]

You will need three equations because there are three things to be determined: firing position, speed and angle. Two equations come from skimming the corners and the other from the minimum speed requirement.

Consider it a math problem, not a physics problem. For a parabola you need three prameters.

As a maths problem it's quite hard. But, if you get the right physical insight ...

 

[PeroK]

@vishnu 73 Here's my thinking about the person on the roof. You are on the ground, firing projectiles. You start from one point, and try all different angles until you get the minimum velocity in that position. Then you move on to a different position.

Meanwhile, the person on the roof sees your projectiles coming up from below them - imagine they only see the projectiles when they are above the height of the roof. What can the person on the roof say about the projectiles that just skim both sides of the roof?

 

[haruspex]

i am not considering this problem first i am considering the simpler problem i posed in post #1

Yes, but I was hoping you would see that the problem is rather simpler than it seems. Indeed, the flat roof case reduces to the standard maximum range problem, which I feel sure you would have met.

 

[timetraveller123]

sorry for the late reply

@PeroK that is a great insight

as far as the person on the person is concerned the projectile has fixed lauching and target points and hence the only parameters that can be changed according to him is the velocity and angle at the corners

so this will be equivalent to minimising the velocity for the guy on the roof

so returning to the actual problem
$v cos \theta = d_x\\ v sin \theta t - \frac{1}{2}g t^2 = d_y\\ t^2 - \frac{2 v sin \theta}{g} t + 2 \frac{d_y}{g}= 0\\ t = \frac{vsin\theta + \sqrt{v^2 sin \theta ^2 - {d_y}^2}}{g}\\ vcos \theta \frac{vsin\theta + \sqrt{v^2 sin \theta ^2 - {d_y}^2}}{g} = d_x\\$
hopefully it is correct taking derivative with respect to theta implicitly
$2 v sin2\theta \frac{d v}{d \theta} + v ^2 cos 2 \theta + (\frac{d v}{d \theta} cos \theta - v sin \theta)\sqrt{v^2 sin \theta ^2 - {d_y}^2} + v cos \theta \frac{2 v \frac{dv}{d \theta}sin ^2 \theta + v ^2 sin2\theta}{2 \sqrt{v^2 sin \theta ^2 - {d_y}^2}} = 0$
setting all dv\dtheta = 0
then theoretically it could be solved but is there an easier method?

 

[PeroK]

sorry for the late reply

@PeroK that is a great insight

as far as the person on the person is concerned the projectile has fixed lauching and target points and hence the only parameters that can be changed according to him is the velocity and angle at the corners

so this will be equivalent to minimising the velocity for the guy on the roof

so returning to the actual problem
$v cos \theta = d_x\\ v sin \theta t - \frac{1}{2}g t^2 = d_y\\ t^2 - \frac{2 v sin \theta}{g} t + 2 \frac{d_y}{g}= 0\\ t = \frac{vsin\theta + \sqrt{v^2 sin \theta ^2 - {d_y}^2}}{g}\\ vcos \theta \frac{vsin\theta + \sqrt{v^2 sin \theta ^2 - {d_y}^2}}{g} = d_x\\$
hopefully it is correct taking derivative with respect to theta implicitly
$2 v sin2\theta \frac{d v}{d \theta} + v ^2 cos 2 \theta + (\frac{d v}{d \theta} cos \theta - v sin \theta)\sqrt{v^2 sin \theta ^2 - {d_y}^2} + v cos \theta \frac{2 v \frac{dv}{d \theta}sin ^2 \theta + v ^2 sin2\theta}{2 \sqrt{v^2 sin \theta ^2 - {d_y}^2}} = 0$
setting all dv\dtheta = 0
then theoretically it could be solved but is there an easier method?

You should try getting rid of the $t$ and having a parabolic equation for $x$ and $y$.

In the case of a flat roof, is maximising the range for a given velocity the same problem as minimising the velocity for a given range?

In the case of the sloping roof can you think of a similar idea?

PS using the parabolic equation for projectile motion is generally very useful for a range of problems.

 

[tnich]

sorry for the late reply

@PeroK that is a great insight

as far as the person on the person is concerned the projectile has fixed lauching and target points and hence the only parameters that can be changed according to him is the velocity and angle at the corners

so this will be equivalent to minimising the velocity for the guy on the roof

so returning to the actual problem
$v cos \theta = d_x\\ v sin \theta t - \frac{1}{2}g t^2 = d_y\\ t^2 - \frac{2 v sin \theta}{g} t + 2 \frac{d_y}{g}= 0\\ t = \frac{vsin\theta + \sqrt{v^2 sin \theta ^2 - {d_y}^2}}{g}\\ vcos \theta \frac{vsin\theta + \sqrt{v^2 sin \theta ^2 - {d_y}^2}}{g} = d_x\\$
hopefully it is correct taking derivative with respect to theta implicitly
$2 v sin2\theta \frac{d v}{d \theta} + v ^2 cos 2 \theta + (\frac{d v}{d \theta} cos \theta - v sin \theta)\sqrt{v^2 sin \theta ^2 - {d_y}^2} + v cos \theta \frac{2 v \frac{dv}{d \theta}sin ^2 \theta + v ^2 sin2\theta}{2 \sqrt{v^2 sin \theta ^2 - {d_y}^2}} = 0$
setting all dv\dtheta = 0
then theoretically it could be solved but is there an easier method?

I can see several things that would make this simpler.
1) Write your equations in terms of horizontal and vertical velocity components ($v_x$ and $v_y$). Dispense with the sines and cosines.
2) Use energy conservation to come up with another equation relating the vertical velocity components at the two edges of the roof.
3) Keep your equation for horizontal displacement (and correct it by putting in $t$ in the appropriate place), but instead of your ballistic equation for change in height, use the ballistic equation for change in vertical velocity.
4) Now with fairly simple algebra you can write an expression for the squared velocity in terms of one unknown (I suggest $v^2_x$) and then minimize it with respect to that variable.

 

[haruspex]

$t^2 - \frac{2 v sin \theta}{g} t + 2 \frac{d_y}{g}= 0\\ t = \frac{vsin\theta + \sqrt{v^2 sin \theta ^2 - {d_y}^2}}{g}$

Check that step. The second line is dimensionally inconsistent.
(Good idea always to check for consistency.)
But as others have posted, it would be better to eliminate t by substituting t=d_x/(v cos(θ)) in the d_y equation.

 

[timetraveller123]

Check that step. The second line is dimensionally inconsistent.
(Good idea always to check for consistency.)
But as others have posted, it would be better to eliminate t by substituting t=d_x/(v cos(θ)) in the d_y equation.

oh you i forgot the t in the very first equation thanks

ok here i try again

$d_x tan \theta - \frac{g}{2 v ^2 cos \theta ^2 } = d_y\\ d_x sec^2 \theta - \frac{g}{2}(\frac{-2}{v^3} \frac{dv}{d \theta} sec^2 \theta + \frac{2 sec^2 \theta tan \theta}{v^2})= 0\\ sec^2 \theta (d_x - \frac{2 tan \theta}{v^2}) = 0\\ \frac{v^2 d_x}{2} = tan \theta\\$
is this correct(hopefully

 

[PeroK]

oh you i forgot the t in the very first equation thanks

ok here i try again

$d_x tan \theta - \frac{g}{2 v ^2 cos \theta ^2 } = d_y\\ d_x sec^2 \theta - \frac{g}{2}(\frac{-2}{v^3} \frac{dv}{d \theta} sec^2 \theta + \frac{2 sec^2 \theta tan \theta}{v^2})= 0\\ sec^2 \theta (d_x - \frac{2 tan \theta}{v^2}) = 0\\ \frac{v^2 d_x}{2} = tan \theta\\$
is this correct(hopefully

Note that a neat idea is to use $z = \tan \theta$ to simplify the differentiation. With this you have the equation:

$y = zx - \frac{gx^2}{2v^2}(1+z^2)$

 

[PeroK]

oh you i forgot the t in the very first equation thanks

ok here i try again

$d_x tan \theta - \frac{g}{2 v ^2 cos \theta ^2 } = d_y\\ d_x sec^2 \theta - \frac{g}{2}(\frac{-2}{v^3} \frac{dv}{d \theta} sec^2 \theta + \frac{2 sec^2 \theta tan \theta}{v^2})= 0\\ sec^2 \theta (d_x - \frac{2 tan \theta}{v^2}) = 0\\ \frac{v^2 d_x}{2} = tan \theta\\$
is this correct(hopefully

That's nearly correct, although $g$ has disappeared!

If you fix that, what's the next step?

 

[haruspex]

$d_x tan \theta - \frac{g}{2 v ^2 cos \theta ^2 } = d_y$

You really must get in the habit of doing consistency checks.
On the left and right you have distances, but the term in the middle is acceleration (L.T^-2) over velocity squared, i.e.1/(L².T^-2). That reduces to L^-1, the inverse of a distance.

 

[timetraveller123]

You really must get in the habit of doing consistency checks.
On the left and right you have distances, but the term in the middle is acceleration (L.T-2) over velocity squared, i.e.1/(L2.T-2). That reduces to L-1, the inverse of a distance.

so sorry for being so careless this time it should be be correct if i am not wrong
this is what i am getting
$\frac{v^2}{g d_x} = tan \theta$
which seems to reduce to maximum range result for theta = 45 so maybe its correct

plugging it back in original equation i am getting
$d _y = \frac{v^2}{2g} - \frac{g d_x ^2}{2 v^2}$
using
$d_y = -(a-c)\\ d_x ^2 =b^2 - (a-c)^2\\$
solving for v ^2
$v^2 = g(b+c - a)$
adding back 2ga for energy conservation
$v = \sqrt{g(a+b+c)}\\$
is this correct