- #1
Jahnavi
- 848
- 102
Homework Statement
Homework Equations
The Attempt at a Solution
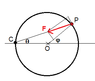
Since the force is always directed towards C , angular momentum about C should be conserved . But that doesn't seem to help as we need the relation at any general angle .
How should I proceed ?