- #1
tangodirt
- 54
- 1
I'm trying to use a second order passive RC filter to attenuate noise in a thermocouple signal. I've heard that using two passive RC filters in series can generate "loading" effects. I'm not sure exactly what this means, except for the output response is different from the theoretical response.
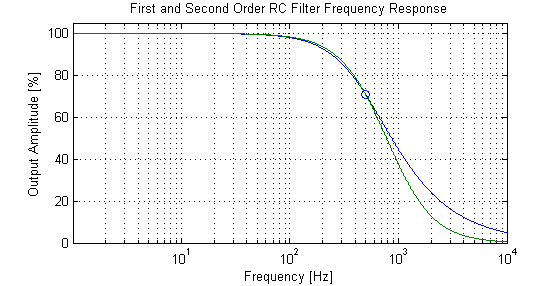
Here is my theoretical response for a 500Hz cutoff frequency:
What effects does loading have on the output response and how can I combat them?
Here is my theoretical response for a 500Hz cutoff frequency:
What effects does loading have on the output response and how can I combat them?