Why Do Path Integrals Involve Multiple Integrations Instead of Simple Summation?

[TimeRip496]

Source: http://web.mit.edu/dvp/www/Work/8.06/dvp-8.06-paper.pdf

Regarding page 5 of 14, I don't understand the multiple integrals thing.

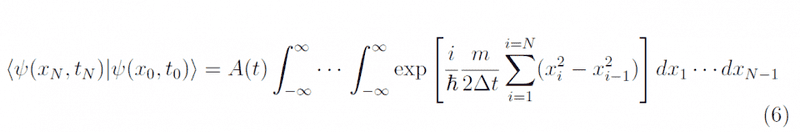
Ain't we supposed to sum up all the paths like in this equation (4)

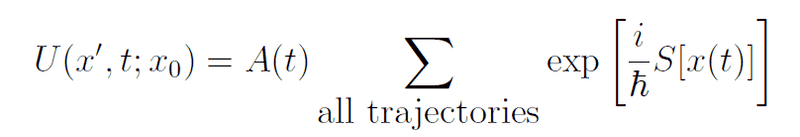but why do they instead multiply and integrate over integration and so on?Also for equation (7)

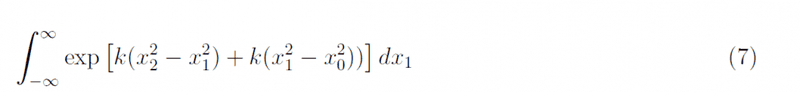, shouldn't it be this

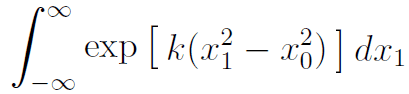instead?

 

[thephystudent]

The sum is just a notation, imagine you would sum all paths over a discrete (t,x) grid. Then summing all the paths would mean for each t-value a summation over all possible x-values.
In the limit when the x-direction becomes continuous, the sums become integrals. In the limit when the t-direction becomes continuous, the number of integrals becomes infinite.

And regarding the second question, those MIT notes are wrong(never thought I'd say this one day :p ). The squares should be outside the parentheses, as in (6) and again in (9)

 

[TimeRip496]

The sum is just a notation, imagine you would sum all paths over a discrete (t,x) grid. Then summing all the paths would mean for each t-value a summation over all possible x-values.

I am sorry but I have difficulty digesting this. Why can't we just sum all the integration of each distinct segment of path, which give each distinct path instead of integrating over each other?

And regarding the second question, those MIT notes are wrong(never thought I'd say this one day :p ). The squares should be outside the parentheses, as in (6) and again in (9)

Even if the squares are outside,my question still remains. As in why does it have x2 when isn't it supposed to just have x1 & x0?

 

[thephystudent]

I am sorry but I have difficulty digesting this.

You should know the double-slit experiment where there you have to sum over the two possible slits the particle can go through. Now imagine two plates behind each other with each one two slits. Now you have to do two summations, one for each plate. Now add an infinite amount of plates, so you get an infinite amount of summations. Next, drill more slits in the plates so each sum should go over more than two possibilities. Now drill an infinite amount of slits till the plates are completely gone and then the sum becomes an integral.

Even if the squares are outside,my question still remains. As in why does it have x2 when isn't it supposed to just have x1 & x0?

Basically, you're "gluing" the piece between x2 and x1 together with the piece between x1 and x0.

 

[TimeRip496]

You should know the double-slit experiment where there you have to sum over the two possible slits the particle can go through. Now imagine two plates behind each other with each one two slits. Now you have to do two summations, one for each plate. Now add an infinite amount of plates, so you get an infinite amount of summations. Next, drill more slits in the plates so each sum should go over more than two possibilities. Now drill an infinite amount of slits till the plates are completely gone and then the sum becomes an integral.

This is a good analogy.
Just to confirm, this ∫e^(i/ћ)S₁ dx₁ is the probability for one segment of a path between the endpoints that can range from -∞ to ∞?

As for the one when you can "glue" the piece between x2 and x1 together with the piece between x1 and x0, it is because they share a similar x1 right? A bit hard to visualise. Besides you know how to convert equation 8 to 9?

 

[vanhees71]

No, this cannot be a probability, because it's a complex number. For a basic derivation and some simple applications of the path-integral formalism, see the introductory Chpt. 1 of my QFT lectures (this 1st chapter is completely only about non-relativistic QM; so you don't need any QFT for it!):

http://fias.uni-frankfurt.de/~hees/publ/lect.pdf

 

[stevendaryl]

I am sorry but I have difficulty digesting this. Why can't we just sum all the integration of each distinct segment of path, which give each distinct path instead of integrating over each other?

I'm not sure I understand your question, but let me illustrate how the integrals come into play by an analogy.

Suppose we are betting on a frog. We have a race track with a starting line at square number 0 and a finish line at square number 100. We put the frog at the starting line, and let the frog take 10 jumps. The frog wins if after 10 jumps, it has made it to the finish line. The oddsmakers need to figure out the probability of the frog winning. They can mathematically describe it by a function $P(x, y, N)$, which is the probability that the frog can get from square $x$ to square $y$ in $N$ jumps. Of course, the number that they are interested in is $P(0,100,10)$. To compute $P(x,y,N)$, they reason as follows:

• On the first jump, the frog will reach some square--0, 1, 2, ..., or 100.
• So there are 101 ways for the frog to win the race: Either he gets to 0 in 1 jump and gets from 0 to 100 in 9 more jumps, or he gets to 1 in 1 jump and gets to 100 in 9 more jumps, etc.
• The probability that the frog wins in the first way is: $P(0, 0, 1) P(0, 100, 9)$
• The probability that the frog wins in the second way is: $P(0, 1, 1) P(1, 100, 9)$
• etc.
• To compute the probability of the frog winning, we just add up the probabilities for each possible way of winning.
• So: $P(0, 100, 10) = \sum_{x_1 = 0\ to\ 100} P(0, x_1, 1) P(x_1, 100, 9)$
• Similarly, $P(x_1, 100, 9) = \sum_{x_2 = 0\ to\ 100} P(x_1, x_2, 1) P(x_2, 100, 8)$
• Continuing to break the number of jumps down, we come to the conclusion that: $P(0, 100, 10) = \sum_{x_1} \sum_{x_2} \sum_{x_3} ... \sum_{x_{9} } P(0, x_1, 1) P(x_1, x_2, 1) ... P(x_9, 100, 1)$, where all the sums are from 0 to 100.

Now, the above calculation is actually an approximation, because we ignored the frog's position within a square. In reality, there is practically a continuum of positions that the frog can be at after one jump. So the summations should actually be replaced by integrals:
$P(0, 100, 10) = \int_{x_1} \int_{x_2} \int_{x_3} ... \int_{x_{9} } dx_1 dx_2 ... dx_9 P(0, x_1, 1) P(x_1, x_2, 1) ... P(x_9, 100, 1)$, where all the integrals are from 0 to 100.

If we had a quantum-mechanical frog, then instead of computing probabilities, we would compute probability amplitudes: Let $G(x,y,t)$ be the probability amplitude that the frog will move from $x$ to $y$ in $t$ seconds. Then:

$G(x, y, t) = \int_{x_1} \int_{x_2} \int_{x_3} ... \int_{x_{N-1} } dx_1 dx_2 ... dx_{N-1} G(x, x_1, \delta t) G(x_1, x_2, \delta t) ... G(x_9, y, \delta t)$

where $\delta t = t/N$

To get the path integral, you write, in the case where $\delta t$ is very small:
$G(x,y,\delta t) \approx C e^{\frac{i L(x,\dot{x}) \delta t}{\hbar}}$ where $C$ is some normalization factor, and $L(x, \dot{x})$ is the classical Lagrangian, and $\dot{x} = \frac{y - x}{\delta t}$. Using properties of exponentials, we can rewrite this as

$G(x, y, t) = \int_{x_1} \int_{x_2} \int_{x_3} ... \int_{x_{N-1} } dx_1 dx_2 ... dx_{N-1} C^{N-1} e^{\frac{i}{\hbar} \sum_{i=0\ to\ N} L(x, \dot{x}) \delta t}$

The sum in the exponential becomes an integral in the limit as $\delta t \Rightarrow 0$:

$G(x, y, t) = \int_{x_1} \int_{x_2} \int_{x_3} ... \int_{x_{N-1} } dx_1 dx_2 ... dx_{N-1} C^{N-1} e^{\frac{i}{\hbar} \int_{0}^t L(x, \dot{x}) dt'}$

 

[TimeRip496]

I'm not sure I understand your question, but let me illustrate how the integrals come into play by an analogy.

Suppose we are betting on a frog. We have a race track with a starting line at square number 0 and a finish line at square number 100. We put the frog at the starting line, and let the frog take 10 jumps. The frog wins if after 10 jumps, it has made it to the finish line. The oddsmakers need to figure out the probability of the frog winning. They can mathematically describe it by a function $P(x, y, N)$, which is the probability that the frog can get from square $x$ to square $y$ in $N$ jumps. Of course, the number that they are interested in is $P(0,100,10)$. To compute $P(x,y,N)$, they reason as follows:

• On the first jump, the frog will reach some square--0, 1, 2, ..., or 100.
• So there are 101 ways for the frog to win the race: Either he gets to 0 in 1 jump and gets from 0 to 100 in 9 more jumps, or he gets to 1 in 1 jump and gets to 100 in 9 more jumps, etc.
• The probability that the frog wins in the first way is: $P(0, 0, 1) P(0, 100, 9)$
• The probability that the frog wins in the second way is: $P(0, 1, 1) P(1, 100, 9)$
• etc.
• To compute the probability of the frog winning, we just add up the probabilities for each possible way of winning.
• So: $P(0, 100, 10) = \sum_{x_1 = 0\ to\ 100} P(0, x_1, 1) P(x_1, 100, 9)$
• Similarly, $P(x_1, 100, 9) = \sum_{x_2 = 0\ to\ 100} P(x_1, x_2, 1) P(x_2, 100, 8)$
• Continuing to break the number of jumps down, we come to the conclusion that: $P(0, 100, 10) = \sum_{x_1} \sum_{x_2} \sum_{x_3} ... \sum_{x_{9} } P(0, x_1, 1) P(x_1, x_2, 1) ... P(x_9, 100, 1)$, where all the sums are from 0 to 100.

Now, the above calculation is actually an approximation, because we ignored the frog's position within a square. In reality, there is practically a continuum of positions that the frog can be at after one jump. So the summations should actually be replaced by integrals:
$P(0, 100, 10) = \int_{x_1} \int_{x_2} \int_{x_3} ... \int_{x_{9} } dx_1 dx_2 ... dx_9 P(0, x_1, 1) P(x_1, x_2, 1) ... P(x_9, 100, 1)$, where all the integrals are from 0 to 100.

If we had a quantum-mechanical frog, then instead of computing probabilities, we would compute probability amplitudes: Let $G(x,y,t)$ be the probability amplitude that the frog will move from $x$ to $y$ in $t$ seconds. Then:

$G(x, y, t) = \int_{x_1} \int_{x_2} \int_{x_3} ... \int_{x_{N-1} } dx_1 dx_2 ... dx_{N-1} G(x, x_1, \delta t) G(x_1, x_2, \delta t) ... G(x_9, y, \delta t)$

where $\delta t = t/N$

To get the path integral, you write, in the case where $\delta t$ is very small:
$G(x,y,\delta) \approx C e^{\frac{i L(x,\dot{x}) \delta t}{\hbar}}$ where $C$ is some normalization factor, and $L(x, \dot{x})$ is the classical Lagrangian, and $\dot{x} = \frac{y - x}{\delta t}$. Using properties of exponentials, we can rewrite this as

$G(x, y, t) = \int_{x_1} \int_{x_2} \int_{x_3} ... \int_{x_{N-1} } dx_1 dx_2 ... dx_{N-1} C^{N-1} e^{\frac{i}{\hbar} \sum_{i=0\ to\ N} L(x, \dot{x}) \delta t}$

The sum in the integral becomes an integral in the limit as $\delta t \Rightarrow 0$:

$G(x, y, t) = \int_{x_1} \int_{x_2} \int_{x_3} ... \int_{x_{N-1} } dx_1 dx_2 ... dx_{N-1} C^{N-1} e^{\frac{i}{\hbar} \int_{0}^t L(x, \dot{x}) dt'}$

Wow this is really good. Thanks a lot!
But i thought $\dot{x} = \frac{y - x}{t}$
Besides do you mind telling me how to get $G(x,y,\delta) \approx C e^{\frac{i L(x,\dot{x}) \delta t}{\hbar}}$? I am a bit fuzzy at the exponential part.

 

[TimeRip496]

No, this cannot be a probability, because it's a complex number. For a basic derivation and some simple applications of the path-integral formalism, see the introductory Chpt. 1 of my QFT lectures (this 1st chapter is completely only about non-relativistic QM; so you don't need any QFT for it!):

http://fias.uni-frankfurt.de/~hees/publ/lect.pdf

Sorry I meant probability amplitude