Pendulum-Spring-Mass System- HELP

[jbroy15]

Hey, I am working on a project for a class (not looking for answers, looking for advice) which involves solving a pendulum-spring-mass system. Pretty much the system is setup like this: point(ish) mass on a spring, moving as a pendulum. We are assuming that the spring stays straight (as a pendulum would) as it swings back and forth.

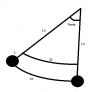
I am taking the length of the spring to be (Lo + L), where L=L(t) (and Lo is the natural position of the spring before any extension or depression). Theta will be T=T(t), arc length will be given as S=S(t)=T*(Lo + L). m is the mass, b is the constant I am applying to the resistance force, k is the spring constant, and g is gravitational acceleration.

I found (with a professor's approval on them) differential equations describing the length and arc length:

mS'' + bs' = -mg sinT

mL'' + bL' + kL = mg cosT

Generally, if L wasn't a function of T, I would introduce S=T(Lo + L) and T=sinT, for small angles (which is the case I am looking at)...but it is, so it creates more problems than solves them. I realized here that I had a slight problem...even with a good amount of trig and triangle equalities. It did occur to me, however, that while T was being used for the main problem... it was also being used for a different pendulum problem.

If we make a new arc length coming out of the end of Lo (and the beginning of L), we have a pendulum with no spring. Which allows us to do the substitution: S₂=T*Lo. This gives us the new DE:

mLo T'' + bLo T' + mgT = 0.

I can solve for T easily, plug it back into the previous DE, solve the previous DE with variation of parameters (or other such solving techniques), and then use the equality: S=T(Lo + L) to solve for L(t). Done and done. EXCEPT, after doing this, I quickly discovered T, S, and L were all void of the spring constant: k. I have initial conditions (which I know don't interfere with the k) and therefore have all of my constants solved for...what did I do wrong?

So far I have no good answer for this...haven't gone to the professor yet, I am attempting to do this as much on my own as possible. Obviously my technique was wrong...I just don't know why or what else to do. Suggestions? And please don't rip apart my project or tell me I am doing something stupid...learning here, so please help me to.

Also, I *think* I uploaded a picture of the general idea of my system.

 

[NateD]

My suggestion would be to look into the Lagrangian approach to solve this system. The Lagrangian approach is a powerful tool used in classical mechanics and can be used to solve problems such as yours. This technique involves introducing an auxiliary function called the Lagrangian that is constructed from the kinetic and potential energies of the system. You can then use the Lagrangian to derive the equations of motion for the system. This approach is particularly useful for systems with a lot of degrees of freedom (such as your pendulum-spring-mass system). I suggest looking into some textbooks or online resources to get a better understanding of how to use the Lagrangian approach. Good luck!