Phi^4 theory and counterterms

[CAF123]

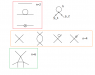
I want to sketch connected graphs in $\phi^4$ theory that contribute to correlation functions involving up to six fields. In $\phi^4$, the cases being are 0 point, 2 point, 4 point and 6 point correlation functions (odd ones don't exist). There are only a few diagrams altogether and I have put them in an attachment - was just wondering if I have all the contributions at tree level and at one loop?

Including renormalized parameters in my lagrangian, I get feynman rules corresponding to counter terms which I have denoted by a circle and a cross inside. I understand that these terms will cancel the tadpole contributions. My integral representation for the tadpole contribution in the n=2 case is like $\int d^4 k /k^2$ in four space time dimensions and is UV divergent. Is it correct to say that this divergence is exactly canceled by the mass counterterm?

Thanks!

 

[vanhees71]

It depends on your renormalization scheme. In a momentum-subtraction scheme the tadpoles are exactly cancelled. Using dimensional regularization and (modified) minimal subtraction or any other mass-independent scheme that's not the case. For details about renormalization (including also $\phi^4$ theory), see

http://fias.uni-frankfurt.de/~hees/publ/lect.pdf

 

[CAF123]

Hi vanhees71,

It depends on your renormalization scheme. In a momentum-subtraction scheme the tadpoles are exactly cancelled. Using dimensional regularization and (modified) minimal subtraction or any other mass-independent scheme that's not the case. For details about renormalization (including also $\phi^4$ theory), see

http://fias.uni-frankfurt.de/~hees/publ/lect.pdf

I have heard of the on shell renormalisation scheme and schemes whereby the $\epsilon$ poles appearing in diagrams are exactly canceled by the renormalization parameters in the lagrangian (they are tuned to absorb the divergencies in $\epsilon$ and make the final answer for the diagram finite and independent of the parameter $\mu$ needed in the dim reg scheme). Are these the schemes you mentioned?

Can I just check that the diagrams I drew in my picture are correct for the tree level and one loop contributions to correlators for $\phi^4$ theory? The case $n=0$ seemed to all include two loops or more so I was not sure about this case.

Thanks!

 

[vanhees71]

In the middle row you also need a coupling-constant counter term.

The on-shell scheme (applicable only for a massive theory) is a special momentum subtraction scheme. So in this case it cancels the tadpole. Just to cancel the poles in $1/\epsilon$ in dimensional regularization defines the minimal-subtraction scheme. Of course the final results still depend on the renormalization scale $\mu$, because it occurs in logarithms. What's independent of $\mu$ are the $Z$ factors and the renormalization-group coefficients (anomalous dimensions). That's because the MS scheme is a mass-independent scheme, and thus the RG coefficients can depend only on the dimensionless coupling, $\lambda$ and thus only implicitly on $\mu$.

 

[mfb]

Shouldn't "-H-" be added to the 6 point correlation function?

 

[CAF123]

In the middle row you also need a coupling-constant counter term.

Ah, what does this look like and what is it for?

Just to cancel the poles in $1/\epsilon$ in dimensional regularization defines the minimal-subtraction scheme. Of course the final results still depend on the renormalization scale $\mu$, because it occurs in logarithms. What's independent of $\mu$ are the $Z$ factors and the renormalization-group coefficients (anomalous dimensions). That's because the MS scheme is a mass-independent scheme, and thus the RG coefficients can depend only on the dimensionless coupling, $\lambda$ and thus only implicitly on $\mu$.

So, just to check, in the on shell scheme for a theory with mass $m$, the $Z$ factors can depend on $\mu$ and contain poles in $\epsilon$ but a final answer can depend on $\mu^2$ (only implicitly through the coupling) and the mass $m^2$ explicitly in logarithms? And the MS scheme (which I am covering next week in class) is applicable to both massive and massless theories with the renormalisation factors $Z$ depending only on $\epsilon$ or $\mu^2$ (implicitly through the coupling) with a final answer depending explicitly on $\mu^2$ through logarithms. Is that all right?

Thanks!

 

[CAF123]

Shouldn't "-H-" be added to the 6 point correlation function?

Yes, I missed that one, that would contribute at tree level but then at one loop correction, I'd be able to insert a tadpole tangential to the propagator and then another tadpole correction on each of the external legs? And each of these would come with a corresponding counterterm diagram?

 

[vanhees71]

Ah, what does this look like and what is it for?

You need the coupling-constant counter-term to cancel the logarithmic divergence of the "dinosaur diagram" (the 2nd diagram in your middle row).

For a complete treatment at the one-loop level, see my lecture notes

http://fias.uni-frankfurt.de/~hees/publ/lectt.pdf

Chapter 5.

So, just to check, in the on shell scheme for a theory with mass $m$, the $Z$ factors can depend on $\mu$ and contain poles in $\epsilon$ but a final answer can depend on $\mu^2$ (only implicitly through the coupling) and the mass $m^2$ explicitly in logarithms? And the MS scheme (which I am covering next week in class) is applicable to both massive and massless theories with the renormalisation factors $Z$ depending only on $\epsilon$ or $\mu^2$ (implicitly through the coupling) with a final answer depending explicitly on $\mu^2$ through logarithms. Is that all right?

Thanks!

In the mass-independent renormalization schemes, among them the MS and $\overline{\mathrm{MS}}$ schemes of dimensional regularization, have the advantage that the (dimensionless!) $Z$'s do not depend on $m$ and thus cannot depend on $\mu$ explicitly but only via the dimensionless compling constant $\lambda$. That's how the scale comes into the game in dimensional regularization. In order to have a dimensionless coupling constant at any space-time dimension $d=4-2\epsilon$ you have to introduce an energy scale $\mu$ and write $\lambda \mu^{2 \epsilon}$ in the regularized integrals. Then you can evaluate the $Z$'s perturbatively using the counter-term procedure and derive the RG coefficients (anomalous dimensions) that determine the running of the coupling, wave-function and mass renormalization. In the MIR schemes the mass counterterm is proportional to the mass, and $\delta m^2=0$. As I said this is explained in much detail in my above linked manuscript in Chpt. 5.

 

[CAF123]

You need the coupling-constant counter-term to cancel the logarithmic divergence of the "dinosaur diagram" (the 2nd diagram in your middle row).

For a complete treatment at the one-loop level, see my lecture notes

http://fias.uni-frankfurt.de/~hees/publ/lectt.pdf

Chapter 5.

Thanks! Ok so in the on shell scheme, for example, this coupling constant term removes the poles in epsilon appearing in the (divergent) result for the dinosaur diagram? So would I just represent this counterterm diagram with four lines coming to a point but with a circle and cross placed at the local interaction vertex?

Also regarding Mfb's point about the inclusion of the tree level -|-|- diagram, at one loop, I could insert tadpole corrections on the propagator there or any of the external lines. Each of these diagrams contained in the connected generating functional $Z(J) = \exp(iW(J))$ also comes with mass counterterms, yes? But I am also thinking, at one loop, I can replace each of these tadpoles with bubble insertions so how do I distinguish between the counterterms introduced for the bubbles and those for the tadpoles?

Thanks!

 

[vanhees71]

The counter term for the vertex is a crossed circle with four legs and just means $-\mathrm{i} \delta \lambda$ (modulo factors).

For the proper vertex functions you can omit all diagrams which fall apart into two or more pieces by just one line, i.e., you need to take into account only amputated one-particle irreducible diagrams to get the contributions to the effective action, which is the functional that determines the counter terms. So in the middle row you have to omit also the two last diagrams.

 

[CAF123]

For the proper vertex functions you can omit all diagrams which fall apart into two or more pieces by just one line, i.e., you need to take into account only amputated one-particle irreducible diagrams to get the contributions to the effective action, which is the functional that determines the counter terms. So in the middle row you have to omit also the two last diagrams.

Yes, sure, but the last two diagrams in the middle row, for example are indeed still generated from $Z(J) = \exp(iW(J))$, it's just they don't contribute to the effective action because they are one particle reducible?

Thanks!

 

[RGevo]

Dear vanhees, caf123,

I'm a little confused my self about the mass dependent schemes.

When I construct the counterterm, these contain both finite, logarithmic mu dependent pieces and associated 1/eps poles (in dim reg).

When I add these graphs to my bare amplitudes, isn't it true that the poles and associated mu dependence in the amplitudes are canceled exactly?

If I choose to work in the MSbar, my counterterms only contain the poles (and 4pi Euler gamma pieces) and hence when I add these to the bare amplitude the result contains mu dependence since it has not cancelled.

Then I thought people would use a coupling constant calculated 1 higher order in the theory. This way it contains mu dependence which cancels to the order of the amplitude and counter term, but not up to oneloop higher. That way, varying the scale in the coupling constants allows you to track the size of possibly missing terms 1 higher order (which should cancel the mu dependence ).

Please let me know if I am misunderstanding something.

 

[vanhees71]

This is a problem with dimensional regularization. It's very convenient technically but not very intuitive. It's much simpler to look at the renormalization in the way of the BPHZ formalism, i.e., you define a renormalization scheme by fixing the divergent proper vertex function at a certain point in momentum and mass space.

In $\phi^4$ theory (despite the vacuum diagrams that are irrelevant for vacuum QFT) the divergent parts are only the two- and four-point function, giving rise to wave-function normalization and mass as well as coupling-constant counterterms, because the two-point function (self-energy) is quadratically and the four-point function logarithmically divergent.

In momentum space we can write the self-energy as $\Sigma(s,m^2)$, where $s=p^2$ is the four-momentum squared (using Lorentz invariance, the only available arguments for a scalar function are $p^2$ and the mass (squared), which is a scalar itself, because there's only one momentum argument in the self energy). The divergent piecses are thus $\Sigma(s)$ itself as well as $\partial_s \Sigma(s)$. Thus the renormalization scheme is defined as soon as I define, how to subtract these pieces. The four-point function can be written as $\Gamma^{(4)}(s,t,u)$ with the usual Mandelstam variables $(s,t,u)$ for the $2 \rightarrow 2$ (elastic) scattering process.

To see, how this works for different schemes, let's discuss some examples

BPHZ scheme (works only for $m^2>0$)
---------------------------------------------------

The BPHZ scheme subtracts the divergent pieces at the point with all external momenta set to 0, i.e.,
$$\Sigma_{\text{BPHZ}}(s)=\Sigma_{\text{reg}}(s)-\Sigma_{\text{reg}}(s=0)-s \partial_s \Sigma_{\text{reg}}(s=0).$$
$$\Gamma_{\text{BPHZ}}(s,t,u)=\Gamma_{\text{reg}}(s,t,u)-\Gamma_{\text{reg}}(s=t=u=0).$$

This scheme can even be used without any regularization by just subtracting the corresponding expressions from the integrands of the loop integrals and then taking the integral. Of course, for diagrams with more than one loops, you have to also take care of all subdivergences (but not overlapping) according to Zimmermann's forest formula (see my manuscript).

You cannot use this scheme at $m^2=0$, because at 0 external momenta the logarithmically divergent pieces are IR divergent, and subtracting at this point thus leads to IR divergences of the entire renormalized pieces (here the four-point function and $\partial_s \Sigma$, which is also logarithmically divergent).

MOM Scheme
----------------

One way out is to subtract at non-zero momenta with all external momenta at some space-like scale $\Lambda$. This introduces a renormalization scale $\Lambda$ into the game, and this is mandatory for the massless case (leading to violation of scale invariance/conformal symmetry and "dimensional transmutation"). This is called the momentum-subtraction scheme. Of course the original BPHZ for the massive case is also a special MOM scheme.

MIR Scheme
---------------

Mass-independent renormalization schemes introduce a mass scale $M^2$ and subtract (at least) the logarithmic divergence at this scale, i.e., you impose the conditions
$$\Sigma(s=0,m^2=0)=0 \; \Rightarrow \delta m^2=0,$$
$$\partial_{m^2} \Sigma(s=0,m^2=M^2)=0 \; \Rightarrow\; \delta Z_m,$$
$$\partial_s \Sigma(s=0,m^2=M^2)=0 \; \rightarrow \; \delta Z_{\phi},$$
$$\Gamma^{(4)}(s=t=u=0,m^2=M^2)=-\lambda \; \Rightarrow \; \delta \lambda.$$
makes $Z_{\phi}$, $Z_m$, and $\delta \lambda$ independent of $M$, i.e., these quantities become only dependent on $M$ via the renormalized coupling constant, $\lambda$. All these quantities are independent of $m$ at all. You can even evaluate the effective action for $m^2<0$, leading to spontaneous symmetry breaking (in the case of simple $\phi^4$ theory of the discrete field-reflection symmetry, which is not too interesting but for the linear $\sigma$ model to an effective description of pions as Goldstone bosons of chiral symmetry).

The MS scheme(s) are not so directly expressible in terms of conditions on the diverging proper vertex functions and thus a bit less transparent to understand, but it's more convenient in practical calculations, at the same time keeping many symmetries valid, particularly (non-chiral) gauge symmetries, and that's why it's used in modern treatments of QFT, particularly in QCD.

 

[CAF123]

Mass-independent renormalization schemes introduce a mass scale $M^2$ and subtract (at least) the logarithmic divergence at this scale, i.e., you impose the conditions
$$\Sigma(s=0,m^2=0)=0 \; \Rightarrow \delta m^2=0,$$
$$\partial_{m^2} \Sigma(s=0,m^2=M^2)=0 \; \Rightarrow\; \delta Z_m,$$
$$\partial_s \Sigma(s=0,m^2=M^2)=0 \; \rightarrow \; \delta Z_{\phi},$$
$$\Gamma^{(4)}(s=t=u=0,m^2=M^2)=-\lambda \; \Rightarrow \; \delta \lambda.$$
makes $Z_{\phi}$, $Z_m$, and $\delta \lambda$ independent of $M$, i.e., these quantities become only dependent on $M$ via the renormalized coupling constant, $\lambda$.

Thanks for the detailed response! I just wanted to ask something about the last renormalisation condition you have stated there. I am computing the vertex function for $\phi^4$ theory as you do in your notes and also in Peskin and Schroder P.326. I write the vertex function as $i\Gamma(p_1,p_2,p_3,p_4) = iZ_{\lambda} \lambda + iV_4(p_1,p_2,p_3,p_4)$ + two other perms. I have solved for $iV_4$ and can get the other perms by momentum conservation as you also note in your manuscript. The problem I am having is now in getting $Z_{\lambda}$. I want to use the condition $\Gamma(p,p,p,p) = \lambda$ (similar to your last condition above) to get $Z_{\lambda}$. This gives me the following equation $$\lambda = iZ_{\lambda}\lambda - \frac{3\alpha}{2}\left(\frac{1}{\epsilon} + 2(1- \frac{1}{f(p^2,m^2)}\tan^{-1} f(p^2,m^2)) - \ln(m^2/\mu^2)\right)$$ with $\alpha = \tilde{\lambda}^2/(4\pi)^2, \tilde{\lambda}^2 = \lambda^2 \tilde{\mu}^{-2}$. So, if I solve for $Z_{\lambda}$ here I am going to get it as a function of $p, \lambda, \epsilon, m$ and $\mu$? It doesn't seem right given what you said above.

Thanks!

 

[vanhees71]

I don't understand your condition. Do you mean it's $\Gamma(0,0,0,0)=0$? Then it's of course a momentum-subtraction (MOM) scheme, and thus your $Z$ and running coupling become dependent on $m$. To get the above version of the mass-independent renormalization (MIR) scheme, you have to set $m^2=M^2$ in the subtracted part, i.e., you calculate
$$\Gamma_{\text{ren}}(p_1,p_2,p_3,p_4) = \Gamma_{\text{reg}}(p_1,p_2,p_3,p_4)-\Gamma_{\text{reg}}(0,0,0,0)|_{M^2=m^2}.$$
You'll see that the $\mu^2$ is canceled as well as the $1/\epsilon$ term. The subtracted coupling-constant counter term is of course independent on $m^2$ but it depends on $M^2/\mu^2$.

In other words, of course you can use dimensional regularization first and then apply any renormalization scheme you like. To evaluate the anomalous dimensions of the RG equations, then you better use the equations for $\Gamma^{(2)}$, $\partial_{p^2} \Gamma^{(2)}$, and $\Gamma^{(4)}=\Gamma$ as explained in Sect. 5.11.1 of my QFT manuscritpt. It's not so easy to work with the counter terms derived from dim. reg., because you cannot take $\epsilon \rightarrow 0$. Of course you can use also the techniques of Sect. 5.11.2 for other than the there explained case of the MS scheme, but it's more complicated than the way in Sect. 5.11.1.

 

[CAF123]

I don't understand your condition. Do you mean it's $\Gamma(0,0,0,0)=0$?

Hmm I did mean what I wrote. Here is my original question: 1) Draw all one-particle irreducible Feynman diagrams contributing to the vertex correction $i\Gamma(p_1, p_2, p_3, p_4)$ through one loop, and write down the corresponding expressions according to the Feynman rules. 2) Renormalize $i\Gamma(p_1, p_2, p_3, p_4)$, determine $Z_{\lambda}$ and $i\Gamma(p_1, p_2, p_3, p_4)$ at one loop using momentum subtraction with the renormalization condition $\Gamma(p, p, p, p) = \lambda$.

So, essentially I have an expression for $i\Gamma$. It is equal to $iZ_{\lambda}\lambda$ + three other terms, where the latter terms are just different permutations of momenta conservation in the dinosaur diagram. Now, to determine $Z_{\lambda}$, what I am going to do is set my answer above to $\Gamma(p,p,p,p)=\lambda$ as instructed and solve for $Z_{\lambda}$. Is this not correct?

Thanks!

 

[vanhees71]

Again, I don't understand this! What do you mean by writing $\Gamma(p,p,p,p)$? If you just set all momenta equal, that doesn't define a single point in momentum space or do you mean some fixed vector $p$? Have you haver had a look at my manuscript? Which textbook are you using?

 

[CAF123]

Again, I don't understand this! What do you mean by writing $\Gamma(p,p,p,p)$? If you just set all momenta equal, that doesn't define a single point in momentum space or do you mean some fixed vector $p$? Have you haver had a look at my manuscript? Which textbook are you using?

I see, yes I have looked at the manuscript but it's proving a little difficulty in trying to connect everything together with what I see in my course - I have attached the relevant lecture notes I am using at the moment. On the second page at the top there, they introduce $V_3(0,0,0) = g$ in the context of an effective 3 point vertex but my question (associated with the four point vertex) specifically tells me to use $\Gamma(p_1,p_2,p_3,p_4)|_{p_1=p_2=p_3=p_4=p} = \Gamma(p,p,p,p) = \lambda$. So yes, It means some fixed vector p I would say. Thanks.

 

[CAF123]

So essentially I am taking my expression, putting all the $p_i$'s to equal $p$ and setting $i\Gamma(p,p,p,p) = i\lambda$. Since I am working at one loop, I can expand $Z_{\lambda} = 1 + Z_{\lambda}^{(1)} \alpha + \dots$, insert this into my expression and work only up to order $\alpha$ and I get that $$Z_{\lambda}^{(1)} = - \frac{3}{2 i \lambda} (\frac{1}{\epsilon} + 2(1- \frac{1}{f(p^2,m^2)}\tan^{-1} f(p^2,m^2)) - \ln(m^2/\mu^2))$$

Is there anything about this calculation that makes it stand out as being incorrect? I don't think it should depend on $\lambda$, because $Z_{\lambda}$ itself is an expansion in $\lambda$ so its coefficients in this perturbative expansion should not be.

Also, the coupling has mass dimension $2\epsilon$ so the factor we introduce is $\lambda^2 = \tilde{\lambda}^2 \tilde{\mu}^{4 \epsilon} \propto \alpha \tilde{\mu}^{4 \epsilon}$. I see this factor introduced in your manuscript but in (5.94) and subsequent displays it seems to be written as $\mu^{2 \epsilon}$. Could you explain this please?

Thanks!

 

[vanhees71]

I only wonder, why it goes with $1/\lambda$. Shouldn't there be factors of $\lambda$ in your diagram (one for each vertex)? Otherwise it's correct, although I find the notation in your manuscript a bit unfortunate. Why don't you use the invariants $s$, $t$, and $u$? The vertex is a scalar and can thus only depend on scalar invariants of the independent momenta. Then you can use a single $p^2=-\Lambda^2$ as a scale.

You have $s=(p_1+p_2)^2=(p_3+p_4)^2$, $t=(p_1-p_3)^2=(p_2-p_4)^2$, $u=(p_1-p_4)^2=(p_2-p_3)^2$. Thus your subtraction point is $s=-4\Lambda^2$, $t=u=0$. Thus you have a MOM scheme at a space-like subtraction point.

 

[CAF123]

I only wonder, why it goes with $1/\lambda$. Shouldn't there be factors of $\lambda$ in your diagram (one for each vertex)? Otherwise it's correct, although I find the notation in your manuscript a bit unfortunate. Why don't you use the invariants $s$, $t$, and $u$? The vertex is a scalar and can thus only depend on scalar invariants of the independent momenta. Then you can use a single $p^2=-\Lambda^2$ as a scale.

Schematically, the four point renormalized vertex at one loop looks like $i\Gamma(p_1,p_2,p_3,p_4) = iZ_{\lambda}\lambda + \sum_{\text{3 diagrams}} \lambda^2(..)$, where the first term is the tree level local four point interaction and the subsequent three other terms are the dinosaur diagram and its momenta permutations. Now, set $Z_{\lambda} = 1 + Z_{\lambda}^{(1)} \alpha$ and $\lambda^2 = \tilde{\lambda^2}\mu^{4 \epsilon} \propto \alpha$. Then the equation to order $\alpha$ is $$i\Gamma(p_1,p_2,p_3,p_4) = i(1+ Z_{\lambda}^{(1)} \alpha) \lambda + \sum_{\text{3 diagrams}} \alpha(..)$$ Then impose the renormalization scheme, $i\Gamma(p,p,p,p) = i\lambda$ so that the equation becomes $$i \lambda = i(1+ Z_{\lambda}^{(1)} \alpha) \lambda + \sum_{\text{3 diagrams}} \alpha(..)|_{p_1=p_2=p_3=p_4=p}$$ Divide throughout by $i\lambda$ and collect terms means I'll have an $i\lambda$ in the denominator of the latter three terms. That's where it came about, but I agree it doesn't make sense. Is my working correct here?

You have $s=(p_1+p_2)^2=(p_3+p_4)^2$, $t=(p_1-p_3)^2=(p_2-p_4)^2$, $u=(p_1-p_4)^2=(p_2-p_3)^2$. Thus your subtraction point is $s=-4\Lambda^2$, $t=u=0$. Thus you have a MOM scheme at a space-like subtraction point.

If I define all my momenta as incoming, then $s=(p_1+p_2)^2, t=(p_2+p_3)^2, u = (p_1+p_3)^2$. Why did you write the momenta scale as $p^2 = -\Lambda^2$? Is that so that it is defined away from the branch cut structure?

Thanks!

 

[vanhees71]

I still don't understand the $1/\lambda$, because the counterterm is $\delta \lambda=\propto \lambda^2$ and thus $\delta Z_{\lambda}=\delta\lambda/\lambda \propto \lambda$.

Anyway, if all your momenta are incoming then your choice is symmetric in the Mandelstam variables and $s=t=u=-4 \Lambda^2$. You choose the momentum spacelike to stay safely from the branch cut, even in the limit $m^2 \rightarrow 0$. At fixed $m^2>0$ you only must have $p^2=\Lambda^2<4 m^2$.

 

[CAF123]

I still don't understand the $1/\lambda$, because the counterterm is $\delta \lambda=\propto \lambda^2$ and thus $\delta Z_{\lambda}=\delta\lambda/\lambda \propto \lambda$.

Ah, I see, so in my notation do you mean I should write $Z_{\lambda} = 1 + Z_{\lambda}^{(1)} \lambda + \mathcal O(\lambda^2)$ and not $Z_{\lambda} = 1 + Z_{\lambda}^{(1)} \alpha+ \mathcal O(\alpha^2)$? This would indeed give my correction to be something independent of $\lambda$. I just wonder though, in the three point vertex in a $\phi^3$ theory, we wrote the effective 3 point vertex like $Z_{g}= 1+ Z_{g}^{(1)} \alpha + ...$. Is there a reason why the first non trivial term here goes as order $g^2$ (ie order $\alpha$) and not $g$?

Anyway, if all your momenta are incoming then your choice is symmetric in the Mandelstam variables and $s=t=u=-4 \Lambda^2$. You choose the momentum spacelike to stay safely from the branch cut, even in the limit $m^2 \rightarrow 0$. At fixed $m^2>0$ you only must have $p^2=\Lambda^2<4 m^2$.

Thanks.

DId you catch my question about what happened to the $\mu^{4 \epsilon}$ term in your manuscript?

Thanks!

 

[vanhees71]

I see, so $\alpha \propto g^2$ as in gauge theories. Then it makes sense. The $\mu^{4 \epsilon}$ get's absorbed into the logarithms when doing the Laurent expansion around $\epsilon=0$. That's why this scale $\mu$ is absolutely necessary in dimensional regularization, because otherwise you'd get some dimensionful arguments in these logarithms, and that must be always wrong. Whenever you see a dimensionful quantity as argument of a logarithm or any other function that's not a power, it must be something wrong or at least sloppily written. You find this, however, often in (even otherwise excellent) QFT books, even in Weinberg's, but it's nevertheless a sin!

 

[CAF123]

I see, so $\alpha \propto g^2$ as in gauge theories.

Yes, so if I start my expansion like $Z_{\lambda} = 1 + Z_{\lambda}^{(1)} \lambda + \mathcal O(\lambda^2)$ instead of $Z_{\lambda} = 1 + Z_{\lambda}^{(1)} \alpha + \mathcal O(\alpha^2)$, where $\alpha \propto \lambda^2$ then my one loop correction $Z_{\lambda}^{(1)}$ to the renormalized vertex $Z_{\lambda}$ is independent of $\lambda$ as I wanted. However, I am trying to understand if there is any reason why in the consideration of the renormalisation of the 3 point vertex in the $\phi^3$ theory, we start the renormalized coupling as $Z_{\lambda} = 1 + Z_{\lambda }\alpha + \mathcal O(\alpha^2)$ i.e the first correction goes as $\lambda^2$ and not as $\lambda$ as in the $\phi^4$ theory case. Is there a reason for this?

The $\mu^{4 \epsilon}$ get's absorbed into the logarithms when doing the Laurent expansion around $\epsilon=0$. That's why this scale $\mu$ is absolutely necessary in dimensional regularization, because otherwise you'd get some dimensionful arguments in these logarithms, and that must be always wrong. Whenever you see a dimensionful quantity as argument of a logarithm or any other function that's not a power, it must be something wrong or at least sloppily written. You find this, however, often in (even otherwise excellent) QFT books, even in Weinberg's, but it's nevertheless a sin!

Yes. I understand that in $\phi^4$ theory, this coupling acquires dimensionality of $2 \epsilon$ in $d=4-2\epsilon$ which we write as $\lambda^2 = \tilde{\lambda^2} \mu^{4 \epsilon}$, with $\tilde{\lambda^2}$ dimensionless. I see in your manuscript you write $\mu^{4\epsilon}$ in (5.93) but in (5.94) it goes to $\mu^{2 \epsilon}$ and in subsequent steps. Why is this so?

Thanks!

 

[vanhees71]

Argh! There was a typo in my manuscript. The point is that you write the Lagrangian as
$$\mathcal{L}=\frac{1}{2} (\partial_{\mu} \phi_0) (\partial^{\mu} \phi_0) + \frac{m_0^2}{2} \phi_0^2 - \frac{\lambda_0}{4!} \phi_0^4 = \frac{Z}{2} (\partial_{\mu} \phi)(\partial^{\mu} \phi) - Z_m m^2 \phi^2-Z_{\lambda} \frac{\lambda \mu^{2 \epsilon}}{4!} \phi^4.$$
This implies
$$\phi_0=\sqrt{Z} \phi, \quad m_0^2=\frac{Z_m}{Z} m^2, \quad \lambda_0=\frac{Z_{\lambda}}{Z^2} \lambda \mu^{2 \epsilon}.$$
So for the $\delta Z_{\lambda}$ you have to take out one factor $\mu^{2 \epsilon}$. This I've done by introducing the scalar function $A$ in (5.90). Now it should be corrected. Thanks for pointing out the typo!

 

[CAF123]

Argh! There was a typo in my manuscript. The point is that you write the Lagrangian as
$$\mathcal{L}=\frac{1}{2} (\partial_{\mu} \phi_0) (\partial^{\mu} \phi_0) + \frac{m_0^2}{2} \phi_0^2 - \frac{\lambda_0}{4!} \phi_0^4 = \frac{Z}{2} (\partial_{\mu} \phi)(\partial^{\mu} \phi) - Z_m m^2 \phi^2-Z_{\lambda} \frac{\lambda \mu^{2 \epsilon}}{4!} \phi^4.$$
This implies
$$\phi_0=\sqrt{Z} \phi, \quad m_0^2=\frac{Z_m}{Z} m^2, \quad \lambda_0=\frac{Z_{\lambda}}{Z^2} \lambda \mu^{2 \epsilon}.$$
So for the $\delta Z_{\lambda}$ you have to take out one factor $\mu^{2 \epsilon}$. This I've done by introducing the scalar function $A$ in (5.90). Now it should be corrected. Thanks for pointing out the typo!

Ok, thanks, so just to see if I understood what you did - In the initial set up of the integral representation for the dinosaur diagram using the feynman rules, in the notation used above you get a factor of $(Z_{\lambda} \tilde{\lambda})^2 = (Z_{\lambda} \lambda \mu^{2 \epsilon})^2 = Z_{\lambda}^2 \lambda^2 \mu^{2 \epsilon} \mu^{2\epsilon}$, where $\tilde{\lambda}$ carries dimensions $2\epsilon$ and $\lambda$ is the dimensionless one. Now, the $\mu^{2\epsilon}$ you extract out is the same $\mu^{2\epsilon}$ you have in the formula $$\lambda_o = \frac{Z_{\lambda}}{Z^2} \lambda \mu^{2\epsilon}?$$

If that is correct, then in a $\phi^3$ theory in $6-2\epsilon$ dimensions, the bare coupling can be written as $g_o = \frac{g \mu^{\epsilon}}{Z^{3/2}} Z_g$. Why, in the calculation of $Z_g$ do we not factor out a $\mu^{\epsilon}$ here?

Thanks!