- #1
wukunlin
Gold Member
- 480
- 117
This is an assignment I'm doing that is due next month but I would like to make an early start because I find most of the materials in this assignment unfamiliar.
The whole questions is composed of 5 parts, most of them I have a rough idea of but there are some bits and pieces I don't really know about since its been a year since my last quantum mechanics paper and 2 years since I last had a lecture in relativistic effects.
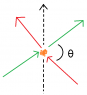
The problem is to do with two 5mW laser beams points at each other as shown in the attached picture as the red and green arrows, representing laser beams of 650nm and 532nm respectively. The orange bits are where the photons interact.
So the first part of the problem.
Calculate the velocity (magnitude and direction) of the CM (I assume centre of mass) System.
[tex]E=h\nu[/tex]
and
[tex]m=\frac{E}{c^2}[/tex]
for relativistic mass
I think to work out the direction I can just treat the photon like two point particles in classical mechanics, which will be similar to the black arrow I have drawn but leaning towards the particle with more relativistic mass.
The magnitude is something I'm not sure about. In classical mechanics, knowing the directions means I can just use geometry to work out the magnitude, but in this case I believe I need to take relativistic effects into account since photons travel at the speed of light.
I looked at this: http://www.numericana.com/answer/relativity.htm#photons
but I'm not sure if that is relavent.
I have also looked at this: http://en.wikipedia.org/wiki/Mass–energy_equivalence#Massless_particles
That doesn't seem to tell me anyway about the velocity of the CoM though,
unless, the CoM also move at the speed of light?
The whole questions is composed of 5 parts, most of them I have a rough idea of but there are some bits and pieces I don't really know about since its been a year since my last quantum mechanics paper and 2 years since I last had a lecture in relativistic effects.
The problem is to do with two 5mW laser beams points at each other as shown in the attached picture as the red and green arrows, representing laser beams of 650nm and 532nm respectively. The orange bits are where the photons interact.
So the first part of the problem.
Homework Statement
Calculate the velocity (magnitude and direction) of the CM (I assume centre of mass) System.
Homework Equations
[tex]E=h\nu[/tex]
and
[tex]m=\frac{E}{c^2}[/tex]
for relativistic mass
The Attempt at a Solution
I think to work out the direction I can just treat the photon like two point particles in classical mechanics, which will be similar to the black arrow I have drawn but leaning towards the particle with more relativistic mass.
The magnitude is something I'm not sure about. In classical mechanics, knowing the directions means I can just use geometry to work out the magnitude, but in this case I believe I need to take relativistic effects into account since photons travel at the speed of light.
I looked at this: http://www.numericana.com/answer/relativity.htm#photons
but I'm not sure if that is relavent.
I have also looked at this: http://en.wikipedia.org/wiki/Mass–energy_equivalence#Massless_particles
That doesn't seem to tell me anyway about the velocity of the CoM though,
unless, the CoM also move at the speed of light?