- #1
Daniel Petka
- 124
- 12
What is the best way to imagine a photon?
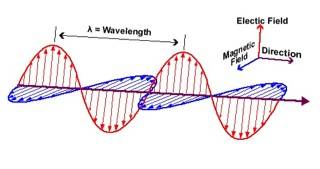
Sometimes I hear that they are simply transverse waves with oscillating EM fields, which just move forward. Other times, though, the photon is said to move along the wave.
The third image reminds me of a probability wave.
So which one is correct?

In fact, none of them really explains, why a photon doesn't interact with a particle that is smaller than its wavelength. I am not able to imagine it well and that confuses me.
Sometimes I hear that they are simply transverse waves with oscillating EM fields, which just move forward. Other times, though, the photon is said to move along the wave.
The third image reminds me of a probability wave.
So which one is correct?
In fact, none of them really explains, why a photon doesn't interact with a particle that is smaller than its wavelength. I am not able to imagine it well and that confuses me.