- #1
emr13
- 33
- 0
1. A square object of mass m is constructed of four identical uniform thin sticks, each of length L, attached together. This object is hung on a hook at its upper corner. If it is rotated slightly and then released, at what frequency will it swing back and forth?
frequency of a physical pendulum:
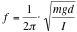
parallel-axis theorem:
I=Icm+MD2
Each thin stick has an I of (1/12)ML2. There are four of them, and the distance from the center of mass of each rod to the center of the square is L/2 so the I for the square (using parallel-axis theorem) is I=(4)((1/12)mL2)+m(L/2)2
Then plug it into the frequency equation...d here is from the axis of rotation to the center of mass, so L/sqrt(2)
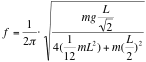
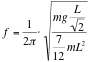
Simplified a little:
Is this right at all? Thanks.
Homework Equations
frequency of a physical pendulum:
parallel-axis theorem:
I=Icm+MD2
The Attempt at a Solution
Each thin stick has an I of (1/12)ML2. There are four of them, and the distance from the center of mass of each rod to the center of the square is L/2 so the I for the square (using parallel-axis theorem) is I=(4)((1/12)mL2)+m(L/2)2
Then plug it into the frequency equation...d here is from the axis of rotation to the center of mass, so L/sqrt(2)
Simplified a little:
Is this right at all? Thanks.