- #1
leafs rule
- 4
- 0
Hi guys. First time posting, and I really need some help on some physics questions. We received some review of about 40 questions for our exam(tomorrow!), and these 3 have stumped me.
1) If there are two points on a conductor each with the same potential...what is the signifigance of these two points? And how much work would be required to move a charge between these two points?
2) A roller coaster reaches the top of a grade at 10 m/s. It then goes downhill and uphill once more. If the second peak is 15m lower than the first, how fast will the roller cosaster be moving at that peak(neglecting friction)?
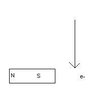
3) If an electrion moving downards past a magnet's south pole, what will be the electron beam's path as it mvoes by the south pole?
Help would be appericatd. Thanks.
1) If there are two points on a conductor each with the same potential...what is the signifigance of these two points? And how much work would be required to move a charge between these two points?
2) A roller coaster reaches the top of a grade at 10 m/s. It then goes downhill and uphill once more. If the second peak is 15m lower than the first, how fast will the roller cosaster be moving at that peak(neglecting friction)?
3) If an electrion moving downards past a magnet's south pole, what will be the electron beam's path as it mvoes by the south pole?
Help would be appericatd. Thanks.
Last edited: