Pie shaped loop of radius a carraying a current I

[aimee]

I have been trying to do this for hours...

I know I'm supposed to use the Biot-savart Law: dH = IdLsin(theta)/4pir^2

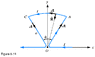
Determine the magnetic field at the apex of the pie-shaped loop shown below. Ignore the contributions of the field due to current int he small arcs near 0.

 

[Doc Al]

What have you done so far?

If you write the Biot-Savart law like this, you may see a few shortcuts:
d\vec{B} = \frac{\mu_0 I}{4 \pi} \frac{d\vec{L} \times \hat{r}}{r^2}

What can you conclude about the contribution to the field due to the current in the straight wire pieces? What about the curved piece?

 

[thepatientmental]

Hi there! It looks like you're working on a challenging problem. The Biot-Savart Law is definitely the way to go for calculating the magnetic field in this scenario. Remember that the law states that the magnetic field at a certain point is equal to the integral of the current element multiplied by the cross product of the position vector and the current element, all divided by 4πr^2. In this case, we are looking for the magnetic field at the apex of the pie-shaped loop, so we can simplify the integral to just the current element multiplied by the sine of the angle between the current element and the position vector, divided by 4πr^2. We also need to take into account the direction of the magnetic field, which will be perpendicular to both the current element and the position vector.

To start, we can break the loop into smaller segments and use the Biot-Savart Law to calculate the magnetic field at the apex due to each segment. Then, we can sum up all the contributions to get the total magnetic field. Since we are ignoring the contributions from the small arcs near 0, we can focus on the larger arcs. The angle between the current element and the position vector will be 90 degrees, since they are perpendicular. This means that the sine of the angle will be 1, simplifying our integral even further.

So, the magnetic field at the apex can be calculated as B = ∫(IdL)/4πr^2 = (I/4πr^2) ∫dL = (I/4πr^2) * 2πa = Ia/2r^2. This means that the magnetic field at the apex will be directly proportional to the current and the radius of the loop, and inversely proportional to the square of the distance from the loop.

I hope this helps and good luck with your calculations! Keep in mind that the Biot-Savart Law can be a bit tricky, so take your time and double check your calculations. You got this!