Calculating Pion Decay Angle in a Moving Reference Frame

[roam]

Homework Statement

A $\pi^0$ at rest decays into two photons, one traveling in the +z direction and the other in the –z direction. What is the angle between the photons in a reference frame moving at speed v=0.99c along the x-axis?

Homework Equations

The Attempt at a Solution

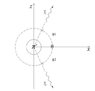
I'm not sure if I understood the problem correctly but I have made a diagram of the situation below. Since the two decay products have an equal mass (zero) their velocity is c, which is greater than that of the parent neutral π meson.

http://imageshack.us/scaled/landing/407/pionp.jpg

I think the problem is asking for the angle which I've labled as θ in my diagram. So how can I work out this angle? Is the question asking for the minimum/maximum decay angle, or a definite angle? (I'm not sure what principles or equations I have to consider).

Any help is greatly appreciated.

 

[mfb]

Is the question asking for the minimum/maximum decay angle, or a definite angle?

There is a single angle as answer, as the geometry of the decay is given.

There are two handy ways to solve it:
1) In the frame of the pion, calculate the 4-momenta of the photons (using energy-momentum-conservation). Transform those to 4-momenta in our lab frame, where the pion frame moves with v=.99c
2) Find the 4-momentum of the pion in our lab frame (it moves with .99c), let it decay in two massless particles (both with a 4-momentum) traveling with opposite z-components of their momentum.

 

[roam]

Thank you very much for the reply. So I'm trying to follow the second option:

Taking c = 1, the 4-momentum for the photon propagating along the +z axis is

$\mathbf{a} = \begin{pmatrix}P^0 \\ P^1 \\ P^2 \\ P^3 \end{pmatrix} = \begin{pmatrix}E/c \\ p_x \\ p_y \\ p_z \end{pmatrix}=\begin{pmatrix}E_1 \\ p_x \\ p_y \\ E_1 \end{pmatrix}$​

This is with the assumption that the photon is moving straight up, and its energy is the same as its momentum as it has no mass. But if it is moving with an angle in the x-z plane (as shown in my drawing) then we will have

$\mathbf{a} = \begin{pmatrix}E_1 \\ E_1 \sin \phi_1 \\ 0 \\ E_1 \cos \phi_1 \end{pmatrix}$​

Now I'm a little confused here about the expression for the second photon along the -z axis. How can we write th 4-momentum expression b for the second photon? Also, is this decay process is completely symmetric?

I think if I have both 4-momenta I can work out the angle as $\theta = \phi_1 + \phi_2$.

 

[mfb]

$\mathbf{a} = \begin{pmatrix}E_1 \\ E_1 \sin \phi_1 \\ 0 \\ E_1 \cos \phi_1 \end{pmatrix}$​

The process is symmetric for the pion (it has to be to conserve energy+momentum), and symmetric in x-direction for us. Therefore, the other photon just has a different sign for its x-component:

$\mathbf{a} = \begin{pmatrix}E_1 \\ -E_1 \sin \phi_1 \\ 0 \\ E_1 \cos \phi_1 \end{pmatrix}$​

 

[roam]

Thank you. I'm a bit confused now, how does the 4-momentum vector of the two photons help in finding the angle θ? Do I need to relate the two vectors by writting an expression for the invariant mass and somehow rearrange it in terms of θ?

Also we could have used E₂ for the second photon (but it is okay as long as the energies are the same).

 

[vela]

Thank you very much for the reply. So I'm trying to follow the second option.

I think you'd find it much more straightforward to analyze and solve if you follow the first option.

If you want to stick with your current approach, back up a second. How are the four-momenta of the photons related to the four-momentum of the pion? What is the four-momentum of the pion?

 

[roam]

I think you'd find it much more straightforward to analyze and solve if you follow the first option.

If you want to stick with your current approach, back up a second. How are the four-momenta of the photons related to the four-momentum of the pion? What is the four-momentum of the pion?

Hi Vela,

I have tried to follow your advice by finding the 4-momentum of the π meson and then relating it to that of the photons.

For the photon where m=0 we had $E_\gamma=P_\gamma$. But this time again using the energy-momentum relationship for a relativistic particle for $\pi^0$ we get:

$E_\pi^2 = p_\pi^2 c^2 + (m_\pi c^2)^2$

or $E_\pi = P_\pi+ m_\pi$ (in units where c = 1)

So, if the pion is moving straight along the +x-axis (not tilted at any angle), its four-momentum I believe is:

$\mathbf{q} = \begin{pmatrix}E_\pi- m_\pi \\ E_\pi- m_\pi \ \cos \phi_1\\ 0 \\ 0 \end{pmatrix}$

Is this correct so far?

Now, how are the 4-momentum of the pion related to the 4-momentum of the photons? I really don't know.

 

[mfb]

$\mathbf{q} = \begin{pmatrix}E_\pi- m_\pi \\ E_\pi- m_\pi \ \cos \phi_1\\ 0 \\ 0 \end{pmatrix}$

Is this correct so far?

What is ϕ?
The energy of the pion (first entry in the vector) is the energy of the pion, $E_\pi$. That will lead to a different expression for its momentum, too. If you work in the lab frame, you can use the known velocity of the pion here.

Now, how are the 4-momentum of the pion related to the 4-momentum of the photons? I really don't know.

What about energy-momentum conservation?

 

[vela]

$E_\pi^2 = p_\pi^2 c^2 + (m_\pi c^2)^2$

or $E_\pi = P_\pi+ m_\pi$ (in units where c = 1)

Are you really claiming that $\sqrt{1^2+1^2} = 1+1 = 2$?

 

[vela]

If you work in the lab frame, you can use the known velocity of the pion here.

For now, though, stick with just writing things in terms of energy and momentum. To keep the algebra simple, it's generally best to avoid using velocities until you absolutely have to.

 

[roam]

What is ϕ?
The energy of the pion (first entry in the vector) is the energy of the pion, $E_\pi$. That will lead to a different expression for its momentum, too. If you work in the lab frame, you can use the known velocity of the pion here.

That is the angle to the x-axis. I have attached a new diagram, indicating the angle ϕ. But I think ϕ=0 for π⁰, so $P_x=\sqrt{E_\pi^2-m_\pi^2}$.

What about energy-momentum conservation?

Yes, for $\pi^0 \to \gamma \gamma$ I think the energy conservation is:

$E_\pi =\sqrt{p_\pi^2 + m_\pi^2}=2 E_\gamma = 2hf$

This has to be satisfied within an uncertainty of $\Delta E = \hbar/2 \Delta t$. But the angle we want doesn't really factor into this equation so I think it is best to use the momentum conservation here?

I'm not sure but I think the momentum conservation is given by:

4-momentum of the neutral π = 4-momenta of two photons

Is this the correct idea?

Are you really claiming that $\sqrt{1^2+1^2} = 1+1 = 2$?

Sorry, it should have been:

$E=[(cp)^2+(mc^2)^2]^{1/2}$

$\therefore \ E_\pi = \sqrt{p_\pi^2 + m_\pi^2}$

$\mathbf{q} = \begin{pmatrix}\sqrt{E_\pi^2- m_\pi^2} \\ \sqrt{E_\pi^2- m_\pi^2}\\ 0 \\ 0 \end{pmatrix}$

 

[mfb]

That is the angle to the x-axis. I have attached a new diagram, indicating the angle ϕ. But I think ϕ=0 for π⁰, so $P_x=\sqrt{E_\pi^2-m_\pi^2}$.

I agree.

$E_\pi =\sqrt{p_\pi^2 + m_\pi^2}=2 E_\gamma = 2hf$

This has to be satisfied within an uncertainty of $\Delta E = \hbar/2 \Delta t$.

It has to be satisfied exactly, as all your particles are real.

I'm not sure but I think the momentum conservation is given by:

4-momentum of the neutral π = 4-momenta of two photons

That is both energy and momentum conservation, as energy is a part of the 4-vector. But the right side is not well-defined like that. How do you compare a single 4-momentum (pion) with two 4-momenta (right side)?

$E=[(cp)^2+(mc^2)^2]^{1/2}$

I agree

$\therefore \ E_\pi = \sqrt{p_\pi^2 + m_\pi^2}$

I would write p in terms of E and not vice versa, but this is possible.

$\mathbf{q} = \begin{pmatrix}\sqrt{E_\pi^2- m_\pi^2} \\ \sqrt{E_\pi^2- m_\pi^2}\\ 0 \\ 0 \end{pmatrix}$

This is wrong. As mentioned before, the energy is E_pi by definition.

 

[roam]

This is wrong. As mentioned before, the energy is E_pi by definition.

Yes my mistake, the first entry shoud have been $E_\pi = \sqrt{p_\pi^2 + m_\pi^2}$ so the 4-momenta is:

$\mathbf{q} = \begin{pmatrix}\sqrt{p_\pi^2+m_\pi^2} \\ \sqrt{E_\pi^2- m_\pi^2}\\ 0 \\ 0 \end{pmatrix}$​

That is both energy and momentum conservation, as energy is a part of the 4-vector. But the right side is not well-defined like that. How do you compare a single 4-momentum (pion) with two 4-momenta (right side)?

I see, so here is my attempt so far:

where the opening angle is θ = 2ϕ, we have:

$\begin{pmatrix}\sqrt{p_\pi^2+m_\pi^2} \\ \sqrt{E_\pi^2- m_\pi^2}\\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix}E_\gamma \\ E_\gamma \sin \phi \\ 0 \\ E_\gamma \cos \phi \end{pmatrix} + \begin{pmatrix}E_\gamma \\ -E_\gamma \sin \phi \\ 0 \\ E_\gamma \cos \phi \end{pmatrix}$​

But this doesn't look right because on the right hand side the fourth row entry reduces to $2E_\gamma \cos \phi$, while on the left hand side the fourth entry is 0! What is wrong with that? Should we also use different signs for the z-components of the photons?

 

[mfb]

Your pion should travel in z-direction, not in x-direction. This will fix your sign problems.

Your way to write the 4-momentum of the pion is quite complicated, but ok.

 

[vela]

Yes my mistake, the first entry shoud have been $E_\pi = \sqrt{p_\pi^2 + m_\pi^2}$ so the 4-momenta is:

$\mathbf{q} = \begin{pmatrix}\sqrt{p_\pi^2+m_\pi^2} \\ \sqrt{E_\pi^2- m_\pi^2}\\ 0 \\ 0 \end{pmatrix}$​

Or you could just write it simply as $q^\mu = (E_\pi, p_\pi, 0, 0)$.

I see, so here is my attempt so far:

where the opening angle is θ = 2ϕ, we have:

$\begin{pmatrix}\sqrt{p_\pi^2+m_\pi^2} \\ \sqrt{E_\pi^2- m_\pi^2}\\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix}E_\gamma \\ E_\gamma \sin \phi \\ 0 \\ E_\gamma \cos \phi \end{pmatrix} + \begin{pmatrix}E_\gamma \\ -E_\gamma \sin \phi \\ 0 \\ E_\gamma \cos \phi \end{pmatrix}$​

But this doesn't look right because on the right hand side the fourth row entry reduces to $2E_\gamma \cos \phi$, while on the left hand side the fourth entry is 0! What is wrong with that? Should we also use different signs for the z-components of the photons?

The three-momentums you have written for the photons are obviously wrong. If $\vec{p}_\gamma$ makes an angle $\phi$ with the x-axis, as you have in your drawing, what's the x-component of $\vec{p}_\gamma$? What's the z-component? Do the signs make sense as you've written them? Both photons travel in the positive-x direction, no? What about their directions along the z-axis?

 

[vela]

Your pion should travel in z-direction, not in x-direction. This will fix your sign problems.

The problem statement, however, specifies that the boost is in the x-direction, so the pion will be moving along the x-axis in the lab frame.

 

[mfb]

Oh, you are right. In that case, the photon momenta are wrong and the pion is correct.

 

[roam]

Thanks guys for the clarification, this is what I've got based on the correct geometry so far:

$\begin{pmatrix}E_\pi \\ p_\pi \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix}E_\gamma \\ E_\gamma \sin \phi \\ 0 \\ E_\gamma \cos \phi \end{pmatrix} + \begin{pmatrix}E_\gamma \\ E_\gamma \sin \phi \\ 0 \\ -E_\gamma \cos \phi \end{pmatrix}$

$\therefore \begin{pmatrix}E_\pi \\ p_\pi \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 2 E_\gamma \\ 2 E_\gamma \sin \phi \\ 0 \\ 0 \end{pmatrix}$​

From the 2nd row we have $p_\pi =2 E_\gamma \sin \phi \implies \phi = \sin^{-1} \left( \frac{p_\pi}{2 E_\gamma} \right)$. Using the first row $E_\pi = 2E_\gamma$, I can write that expression in terms of only E_π:

$\phi = \sin^{-1} \left( \frac{\sqrt{E_\pi^2 - m_\pi^2}}{E_\pi} \right)$​

I made this simplification because we don't know the photon frequency to work out $E_\gamma = hf = \hbar \omega$. But to find a numerical value for the angle I need to know the pion's momentum to work out E_π. So how can I find this?

And how does the given speed of the pion (0.99c) factor into the calculation? Can I just use the mv relationship? (According to my textbook π meson has a mass of 139.6 MeV/c²).

 

[mfb]

The velocity allows to calculate energy and momentum of the pion.
With $\gamma = \frac{1}{\sqrt{1-v^2}}$:
$E=\gamma m_\pi$
$p=\gamma m_\pi v$

 

[vela]

Using the first row $E_\pi = 2E_\gamma$, I can write that expression in terms of only E_π:

$\phi = \sin^{-1} \left( \frac{\sqrt{E_\pi^2 - m_\pi^2}}{E_\pi} \right)$​

Note that according to your expression that if the pion is at rest so that $E_\pi = m_\pi$, the angle is $\phi=0$.

 

[roam]

The velocity allows to calculate energy and momentum of the pion.
With $\gamma = \frac{1}{\sqrt{1-v^2}}$:
$E=\gamma m_\pi$
$p=\gamma m_\pi v$

Thanks, but I have tried two different methods and I am getting two different values for the angle:

Method 1: Using the relativistic equations you have mentioned I worked out:

$E_{\pi^0} = \frac{135}{\sqrt{1-0.99^2}}= 956.98 \ MeV$

$p_{\pi^0} = \frac{135 \times 0.99}{\sqrt{1-0.99^2}}= 947.41 \ MeV/c$

Using the fact that $E_\pi = 2 E_\gamma$ I can re-write the expression

$\phi = \sin^{-1} \left( \frac{p_\pi}{2E_\gamma} \right)= \sin^{-1} \left( \frac{p_\pi}{E_\pi} \right) = 81.89°$

$\therefore \ \theta = 2 \times 81.89 = 163.78°$

Method 2: I have also figured out the energy, momentum, and the frequency of the photons (minimum values required):

Since $M_{\pi^0} =135 MeV/c^2$, we have $E_\gamma = 135/2 = 67 5 MeV$ for each photon. Also

$p_\gamma= \frac{E_\gamma}{c} = 67.5 \ MeV/c$, and $f=\frac{E_\gamma}{h}= 1.63 \times 10^{22} \ Hz$

Now using this E_γ I get a different value for the angle:

$\phi = \sin^{-1} \left( \frac{p_\pi}{2E_\gamma} \right)=44.5°$

$\therefore \ \theta = 89.14°$

So, why do I get different solutions? And which is the correct approach?

Note that according to your expression that if the pion is at rest so that $E_\pi = m_\pi$, the angle is $\phi=0$.

Yes, I have noted that. But I simply made the substitution $p = \sqrt{E^2_\pi - m^2_\pi}$ into the expression for the angle and that is what I've got. What's is the mistake here?

 

[mfb]

Method 2 mixes two different reference frames. The photon energy is calculated in the pion rest frame, but the pion momentum is expressed in our lab frame. It is meaningless to divide them.

And I think you need the cosine instead of the sine in method 1.

 

[vela]

Yes, I have noted that. But I simply made the substitution $p = \sqrt{E^2_\pi - m^2_\pi}$ into the expression for the angle and that is what I've got. What's is the mistake here?

Your four-momenta for the photons are still wrong.

 

[roam]

Method 2 mixes two different reference frames. The photon energy is calculated in the pion rest frame, but the pion momentum is expressed in our lab frame. It is meaningless to divide them.

And I think you need the cosine instead of the sine in method 1.

Oops I didn't notice that. Thanks it makes perfect sense now!

Your four-momenta for the photons are still wrong.

Right, so I have swapped the E_γ sin ϕ and E_γ cos ϕ, so the combined 4-momentum of the photons is:

$\begin{pmatrix}E \\ P_x \\ P_y \\ P_z \end{pmatrix}=\begin{pmatrix}E_\gamma \\ E_\gamma \cos \phi \\ 0 \\ E_\gamma \sin \phi \end{pmatrix} + \begin{pmatrix}E_\gamma \\ E_\gamma \cos \phi \\ 0 \\ -E_\gamma \sin \phi \end{pmatrix}=\begin{pmatrix}2E_\gamma \\ 2E_\gamma \cos \phi \\ 0 \\ 0 \end{pmatrix}$

$\therefore \ \phi = cos^{-1} \left( \frac{p_\pi}{2E_\gamma} \right) = cos^{-1} \left( \frac{p_\pi}{E_\pi} \right) = 8.1°$​

Therefore we have θ≈16°. But this angle is very small. Is this a normal and reasonable value for this angle?

 

[mfb]

For a high-energetic pion (~1 GeV), it looks reasonable.
Well, high-energetic is relative, at the LHC this would be a very slow pion ;).

 

[roam]

Yes I see. Anyway thank you very much for your help, I really appreciate it. :)