- #1
CollegeStudent
- 109
- 0
Homework Statement
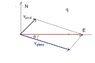
A pilot needs to fly his plane to a location due east as fast as possible. The plane is capable of flying at a top speed of 140 km/h in still air. In this case the wind is blowing exactly NE at 42.5 km/h. In which direction should the pilot point the plane? What will be the planes speed toward its destination?
Homework Equations
The Attempt at a Solution
Well all I have here is the diagram that I drew on the XY plane, with the plane starting at 0 and a vector going east at 140 km/h...and another vector going from the origin to NE at 45°... so the resultant vector should be the I hats and J hats added...so for the magnitude its the i hat and j hat squared and the square root of that...and the angle is y hat over i hat which would be the 45.
Since I'm looking for what direction the pilot needs to fly in order to end up at the destination...shouldn't the resultant vector be the negative...(well opposite) of the vector I had just figured out? And the angle should be the 45 from 360 since its basically going from quadrent 1 to quadrent 4? Am I heading in the right direction here?