Plank leaning against a wall

[Tanya Sharma]

Homework Statement

A plank of length 2L leans against a wall.It starts to slip downward without friction.At what fraction of the initial height does the top of the plank lose contact with the wall .

Homework Equations

The Attempt at a Solution

Let the normal force from the vertical wall on top of the plank be N₁.
Let the normal force from the floor on bottom of the plank be N₂.
Let x and y represent the coordinate of the CM with origin at the bottommost point of the wall.
Let θ be angle which plank makes with the floor at any instant.

The top of the plank loses contact when N₁ = 0.

Now,we have

N₂-Mg = Md²y/dt² (1)

N₁ = Md²x/dt² (2)

N₁Lsinθ-N₂LCosθ = [M(2L)²/12]d²θ/dt²

On simplifying , N₁Lsinθ-N₂LCosθ = (ML²/3)d²θ/dt² (3)


Another relation we can obtain is x=Lcosθ

Differentiating,dx/dt = -Lsinθ(dθ/dt)

Again differentiating , d²x/dt² = -L[cosθ(dθ/dt)²+sinθd²θ/dt²] (4)

How should I proceed further ?

I would be grateful if some member could help me with the problem .


Edit :Fixed errors .Erroneously typed d²x/dt² in place of d²y/dt² and vica versa .

 

[Chestermiller]

Tanya,

Good start. You need to express both x and y in terms of θ. (Incidentally, in the coordinate system you are using, shouldn't x = Lsinθ)? Once you have the second derivatives of x and y with respect to t expressed in terms of the time derivatives of θ, you can substitute these into eqns 1 and 2, and solve for N1 and N2. You then substitute these results into the moment balance. This gives an equation entirely in terms of θ.

Chet

 

[TSny]

I believe x = Lcosθ is correct for the x coordinate of the cm. [Edit: Oh, I now see the confusion. Equations (1) and (2) imply x is vertical and y is horizontal, while x = Lcosθ implies x is horizontal.]

I think you can avoid the force and torque equations (1) and (3) by just using energy along with your equation (4).

 

[Tanya Sharma]

Sorry for the needless confusion in OP .I have fixed the errors .

 

[Tanya Sharma]

I believe x = Lcosθ is correct for the x coordinate of the cm. [Edit: Oh, I now see the confusion. Equations (1) and (2) imply x is vertical and y is horizontal, while x = Lcosθ implies x is horizontal.]

I think you can avoid the force and torque equations (1) and (3) by just using energy along with your equation (4).

For using energy should I use : Loss in PE = Gain in Kinetic energy

But then , I am not sure what is the initial position of the plank .Is it vertical or is it at an arbitrary angle, say α

 

[TSny]

For using energy should I use : Loss in PE = Gain in Kinetic energy

Yes.

But then , I am not sure what is the initial position of the plank .Is it vertical or is it at an arbitrary angle, say α

Assume it's an arbitrary angle. It will still work out nicely.

 

[Tanya Sharma]

Let the initial angle be α then,using COE

mgL(sinα-sinθ) = (2/3)ML²(dθ/dt)²

Is it correct ? If yes ,how to proceed further ?

 

[Chestermiller]

Let the initial angle be α then,using COE

mgL(sinα-sinθ) = (2/3)ML²(dθ/dt)²

Is it correct ? If yes ,how to proceed further ?

Did the steps I outlined in my post #2 not work?

 

[TSny]

That looks good.

What do your equations (2) and (4) tell you at the instant the plank loses contact with the vertical wall?

 

[TSny]

Did the steps I outlined in my post #2 not work?

I apologize for redirecting Tanya towards energy concepts. I happened to find the energy approach to be a nice way to do it. But, of course, the torque and force equations should work, too.

 

[Tanya Sharma]

Did the steps I outlined in my post #2 not work?

Since I had erroneously interchanged d²x/dt² with d²y/dt² in OP ,when I first tried the approach outlined by you ,ended up with a complicated DE .But that is mistake on my part .

I will try again and post the working

 

[Tanya Sharma]

That look's good.

What do your equations (2) and (4) tell you at the instant the plank loses contact with the vertical wall?

This is what i am getting

d²θ/dt² + (3g/2L)cotθ(sinα-sinθ) = 0

Is it correct ?

 

[TSny]

This is what i am getting

d²θ/dt² + (3g/2L)cotθ(sinα-sinθ) = 0

Is it correct ?

Yes.

 

[Tanya Sharma]

Now comes the most difficult part ,solving the DE .

This looks to be a second order DE .But the second term is confusing me.

I will have to look at some reference .Could you please help me identify the DE and the method I have to use .

 

[TSny]

You can avoid solving a DE. Can you see a way to use your energy equation to obtain an expression for $\ddot{θ}$?

 

[Tanya Sharma]

You can avoid solving a DE. Can you see a way to use your energy equation to obtain an expression for $\ddot{θ}$?

This is simply outstanding .

Excellent thinking TSny !

Nevertheless ,how can we solve the DE ?

 

[TSny]

Nevertheless ,how can we solve the DE ?

I don't know. I don't think $\theta$ as a function of time would be very simple.

 

[Tanya Sharma]

:rofl:

terrific sense of humour...

 

[Tanya Sharma]

One thing I need to clarify is that θ is measured from the horizontal with clockwise being the direction of increasing θ .

Does that mean direction of increasing θ has to be considered positive ?
Does this reflect on the direction of torque as well with clockwise torque being considered positive and ccw negative ?

Even though I have used this I am having a little doubt .

 

[haruspex]

I don't know. I don't think $\theta$ as a function of time would be very simple.

I got that time is proportional to ∫cosec(θ/2).dθ, where θ is the angle to the vertical. This is with being vertical initially. That makes sense in that if it really started from vertical with no initial speed then it would take an infinite time.

 

[TSny]

I got that time is proportional to ∫cosec(θ/2).dθ, where θ is the angle to the vertical. This is with being vertical initially. That makes sense in that if it really started from vertical with no initial speed then it would take an infinite time.

Yes. For general starting points, it looks like you might get elliptic integrals of some sort.

 

[ehild]

Well, it is difficult to follow the thread without a a picture showing what is meant positive and negative (upward and to the right in the picture, counter-clockwise for the angle).

If you use the angle from the vertical, it is zero initially, and increases anticlockwise with time .

You have two equations for the acceleration of the CM

$$m\ddot x=N_x$$
$$m\ddot y=N_y-mg$$

and one for the angular acceleration (with respect to the CM)

$$\frac{mL^2}{3}\ddot\theta=N_y L\sin(\theta)-N_x L \cos(\theta)$$

From the geometry, x=Lsin(θ), y=Lcos(θ). Substitute the second derivatives into the first equations, then substitute the expressions of Nx and Ny into the third one. You get a very simple second order de for theta(t) *(I do not show ). You need theta when Nx=0. You certainly know the following trick, but I write it just for case...

dθ/dt=ω. Your equation * does not have t explicitly. You can consider ω as function of θ.

$$\ddot \theta= \dot \omega = \frac{d \omega}{d \theta}\frac{d \theta}{d t}= \frac{d \omega}{d \theta}\omega =0.5 \frac{d (\omega^2)}{d \theta}$$
Integrating and using that initially θ=0 and ω=0, you get ω² as function of θ.
Now use the condition for Nx=0.

ehild

 

[Tanya Sharma]

*(I do not show )

This doesn't look appropriate .

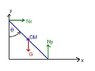
suits you well .

 

[ehild]

Have you got that equation? I would like to see it, please, to check if my one is correct.:shy:

ehild

 

[Tanya Sharma]

Please give me some time .

 

[Tanya Sharma]

The DE is d²θ/dt²+2tanθ(dθ/dt)² = 0 .

 

[ehild]

It is not that equation I meant. There must be a "g" somewhere in it. It is best to show your work in detail.

What did you get for the d²x/dt² and d²y/dt² in terms of theta and derivatives?ehild

 

[Tanya Sharma]

These are the relations I have been working with . θ is the angle which the plank makes with the horizontal .CW sense is treated positive .

N₂-Mg = Md²y/dt² (1)

N₁ = Md²x/dt² (2)

N₁Lsinθ-N₂LCosθ = (ML²/3)d²θ/dt² (3)

d²x/dt² = -L[cosθ(dθ/dt)²+sinθd²θ/dt²] (4)

d²y/dt² = L[-sinθ(dθ/dt)²+cosθd²θ/dt²] (5)

I solved the problem using TSny's approach where energy equation was combined with equation (2) and (4) .

There I got the DE d²θ/dt² + (3g/2L)cotθ(sinα-sinθ) = 0 . Here 'α' is the angle which plank makes ,initially .

I don't know how to solve this DE .But to arrive at the answer solving it was not required.TSny's hint in post #15 worked quite well .

 

[ehild]

I see.
The energy conservation is a first integral of the equation of motion, and it was derived using the transformation dv/dt=dv/dx v. It is a method to make a first-order equation from second order one.

With the method I outlined I got the equation $$\frac{g}{L} \sin (\beta)= \frac{4}{3}\ddot \beta$$, where β is the angle with the wall.
if ω=dβ/dt, $\ddot \beta = \frac{d\omega}{d \beta} \omega$,

$$\frac{g}{L} \sin (\beta)= \frac{4}{3} \frac{d\omega}{d \beta} \omega$$

Integrating: $\frac{g}{L} (\cos (\beta_0)-\cos (\beta))= \frac{2}{3} \omega^2 =\frac{2}{3}(\dot \beta)^2$

Plugging in the expressions for dβ/dt and d²β/dt² into the equation for the horizontal normal force , we get the final angle.
ehild

 

[Tanya Sharma]

Hi TSny...

Could you respond to post #19

 

[TSny]

One thing I need to clarify is that θ is measured from the horizontal with clockwise being the direction of increasing θ .

Does that mean direction of increasing θ has to be considered positive ?

Yes, cw would be the positive direction for θ.

Does this reflect on the direction of torque as well with clockwise torque being considered positive and ccw negative ?

Yes. I believe you set up your torque equation with the correct signs.