- #1
fauxtex
- 5
- 0
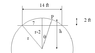
I am an artist, I know a little about math but apparently not enough and I need some help. I am painting a mural on a domed ceiling. The dome is circular, it is 14' in diameter and gradually goes up to 2' high in the center. I need to "cut" this dome into 6 or 8 equal "pie" shapes in order to make a template to transfer my design onto the ceiling. I am stumped as to how to figure the exact shape and size of each of these pieces. Can anyone help me out? Please?
No, I'm not smarter than a fifth grader!
No, I'm not smarter than a fifth grader!