- #1
princes.fiona
- 10
- 0
i have an assignment due this thursday, it has 9 questions, i was able to solve five of them. but for some reason i missed most of the classes in second term so i don't understand anything about the last four questions. the questions are:
Question 1:
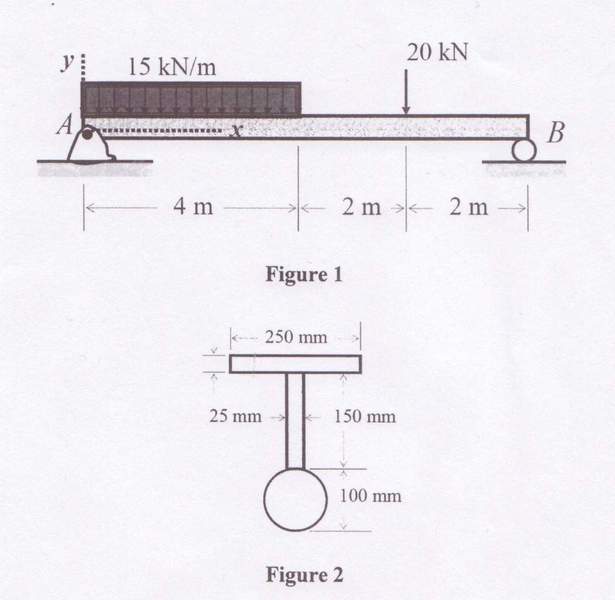
A beam is simply supported and loaded as shown in figure 1a. the cross section of the beam is shown in figure 1b. the beam is made of steel with E= 205 GN/m^2
Find:
(a) The end reactions
(b) The second moment of area for the beam about its centroid
(c) The position and magnitude of the maximum deflection of the beam
Question 2:
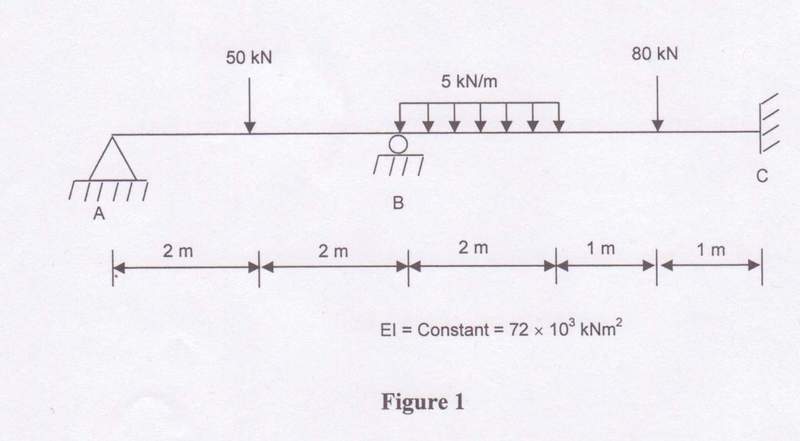
Figure 2 shows a continuous beam with two point loads and a distributed load. The weight of the beam is negligible by comparison. The foundations at supports A and B were not absolutely rigid and there was some deflection at these positions when the loading was applied.
Support A settled by 5mm and support B settled by 2mm
The flexural rigidity of the beam is 72MN/m^2
(a) Calculate the reactions at A, B and C, including the applied moment at C.
(b) Find the deflection at 50kN
Question 3:
A semi-circular arch of uniform rigidity, having one end hinged and other end placed on roller, is subjected to a horizontal force P and a vertical downward load W at crown C in the middle. The radius of the arch is R and the modulus of rigidity of the cross section is EI.
Find a formula for the horizontal displacement of the roller end, B.
Question 4:

A 2380 Nm torque is applied to gear D due to input torque from the motor at A, as shown in figure 4. Shafts 1 and 2 are both solid steel, 44 mm in diameter and 600 mm long. Gear B has a diameter of 250 mm and gear C has a diameter of 350 mm. The shear modulus G for steel is 80GN/m^2
Find out:
(a) the maximum stress in shaft 2
(b) the maximum stress in shaft 1
(c) the rotation angle of gear D relative to the motor at A, due to the loading.
these problems may include the topics of stress, deflection, beams, macaulays method etc. i attended all the classes in first term and solved all the question about balancing, gear trains etc, but i couldn't attend many classes in second term where thiese topics were covered so i couldn't solve these one's. please help me with my assignment. i tried to do it with my 1st years knowledge about beams but couldn't do it. a attched 3 figures related to these questions.
thanks a lot for your help!:!)
Question 1:
A beam is simply supported and loaded as shown in figure 1a. the cross section of the beam is shown in figure 1b. the beam is made of steel with E= 205 GN/m^2
Find:
(a) The end reactions
(b) The second moment of area for the beam about its centroid
(c) The position and magnitude of the maximum deflection of the beam
Question 2:
Figure 2 shows a continuous beam with two point loads and a distributed load. The weight of the beam is negligible by comparison. The foundations at supports A and B were not absolutely rigid and there was some deflection at these positions when the loading was applied.
Support A settled by 5mm and support B settled by 2mm
The flexural rigidity of the beam is 72MN/m^2
(a) Calculate the reactions at A, B and C, including the applied moment at C.
(b) Find the deflection at 50kN
Question 3:
A semi-circular arch of uniform rigidity, having one end hinged and other end placed on roller, is subjected to a horizontal force P and a vertical downward load W at crown C in the middle. The radius of the arch is R and the modulus of rigidity of the cross section is EI.
Find a formula for the horizontal displacement of the roller end, B.
Question 4:
A 2380 Nm torque is applied to gear D due to input torque from the motor at A, as shown in figure 4. Shafts 1 and 2 are both solid steel, 44 mm in diameter and 600 mm long. Gear B has a diameter of 250 mm and gear C has a diameter of 350 mm. The shear modulus G for steel is 80GN/m^2
Find out:
(a) the maximum stress in shaft 2
(b) the maximum stress in shaft 1
(c) the rotation angle of gear D relative to the motor at A, due to the loading.
these problems may include the topics of stress, deflection, beams, macaulays method etc. i attended all the classes in first term and solved all the question about balancing, gear trains etc, but i couldn't attend many classes in second term where thiese topics were covered so i couldn't solve these one's. please help me with my assignment. i tried to do it with my 1st years knowledge about beams but couldn't do it. a attched 3 figures related to these questions.
thanks a lot for your help!:!)