Why Is Understanding the Process Behind Vector Addition Crucial?

[jimmyly]

Hey all, i am just starting out physics so this is very basic stuff. i am having troubles understanding adding vectors. i can do simple ones like a car travels 10km N and 24 km E, find the the total displacement. i understand that. But once i have to add more than 2 vectors together i get very frustrated and i am at the point where i am wanting to punch walls and scream. This is MAINLY because of my teacher. He tells us "okay to find the x component you use Cos and to find the y component use sine. then you use the Pythagorean theorem to with the x component and y component to find the resultant" blah blah blah. i have 100% in precalculus 12 right now so math is not the problem. i know how to do every step. i get the right answer in the end. BUT

the problem:
i don't give two sh*ts about getting questions right. i am so upset because i don't understand WHY we do each step. i asked him before can you explain to me on the board each step so i can have a clear picture of it rather than you just using your excel program and telling us to use cos and sine to find the answer and actually GO INTO the problem and teach me how and why we do each step. and he says well with this many vectors it will take awhile to draw out each vector and do each one invdividually.

i always try to visualize everything i learn in my head or at least try to understand what is going on. but i am having great difficulties understanding adding more than 2 vectors. i don't want to just memorize cos for x and sin for y cause to me that's a load of bullsh*t because i am not learning anything. i am simply plugging numbers into formulas.

so here is a very simple question:

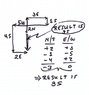
on a trip to the supermarket, you walk 2 blocks N, 3 blocks E, 1 block S, 5 blocks W, 4 blocks S, then 2 blocks E. what is the shortest way home?

i know the answer. i have no problem getting the answer. but my main concern in not getting a question correct rather i want to understand how and why we take each step.

if anyone has a more simple way of doing it please share, i want to understand. not just use this use that plug in here plug that there.

thank you

 

[TSny]

Each displacement vector carries you east a certain amount and/or north a certain amount. (West would be considered a negative amount east, etc.) For a displacement in an arbitrary direction (angle), use trig to find how much east and how much north the vector takes you. That's where the sine and cosine of the angle comes in.

Adding another vector just takes you some additional amount E and additional amount N. Same for the third vector and so on. So, you should be able to see that the total amount that you go east is just the sum of how much each individual vector carries you east. Same for north.

If you know the total amount you end up going east and the total amount that you end up going north, then you should be able to figure out where you end up in relation to where you started (think of a right triangle with one leg representing total amount east and the other leg total amount north.) Then you can figure out the shortest distance to get back home (Pythagoras).

 

[phinds]

Could be I'm not getting what it is that you are having difficulty with, but here's my take. The trig is just to get you the XY sides of each vector. In your example, you already HAVE those, so you don't need any trig:

All vector additions are just additions of all the X movements and all the Y movements to total up to one final vector.

 

[CWatters]

because of my teacher. He tells us "okay to find the x component you use Cos and to find the y component use sine. then you use the Pythagorean theorem to with the x component and y component to find the resultant" blah blah blah.

Ok what he's trying to tell you here is this..

It's easy to add two vectors that are orthogonal because you can use pythagorous. So he's breaking down each original vector into orthogonal components. Then adding up those components and finally applying pythagorous.

Basically he's turning a vector that points say North East into two vectors, one that points North and the other that points East using trig. If you convert all the original vectors the same way it's easy to add the components.

bit like adding equations..

6x + 3y
4x + 2y

can be done because both at in terms of x and y

= 6x + 4x + 3y +2y
= 10x + 5y

 

[NascentOxygen]

He tells us "okay to find the x component you use Cos and to find the y component use sine. then you use the Pythagorean theorem to with the x component and y component to find the resultant"

You must sketch the diagram to see whether it's sin or cosine that is needed. Learning his "rule" as rôte will not serve you well. It holds only where the angle is given w.r.t. the x-axis. There is nothing to say the angle can't be given w.r.t. the y-axis, so sometimes it is, if only to trap the unwary.

 

[CWatters]

Indeed. Sometimes it's better to choose a co-ordinate system that is parallel and orthogonal to one of the original vectors. Convert all the vector to components in that co-ordinate system then add the components.

 

[jimmyly]

thank you everyone. i think i got it now!