How to Calculate Flux Density of Light Passing Through Two Parallel HN-32 Sheets

[roam]

Homework Statement

I need some help understanding the following solved problem:

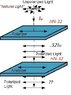
If light that is initially natural and of flux density $I_i$ passes through two sheets of HN-32 whose transmission axes are parallel, what will be the flux density of the emerging beam?

Solution: $64 \% (32 \% \ I_i) = 21 \% I_i$ leaves the second filter.

I don't understand where the "64%" term comes from.

The Attempt at a Solution

If I understand correctly, using a HN-32 sheet means that each filter passes 32% of the incident light. So when natural light enters the first one only 32% leaves it so a flux density of $32 \% \ I_i$ enters the second filter. This light is a P-state or linearly polarized. So I guess the second sheet must take away another 32%, right?

And the rest of the light (68%) must have been tilted toward the extinction axis so it didn't make it through. Therefore I get 32%(32%I_i). So how did they get that answer, and where did the 64% come from?

 

[TSny]

An HN-32 filter will pass 32% of "natural" light where "natural" means unpolarized. But once the light passes the first filter it will then be polarized. So, you need to think about what percentage of the polarized light will get through the second filter.

 

[roam]

An HN-32 filter will pass 32% of "natural" light where "natural" means unpolarized. But once the light passes the first filter it will then be polarized. So, you need to think about what percentage of the polarized light will get through the second filter.

First, if light will be polarized by passing through the first filter, then why is the 32% unpolarized? I thought only the component of light parallel to the transmission axis of the polarizer will be passed on (assuming no absorption). So whatever is passed on is somehow polarized.

Anyway since each filter passes 32% of the natural light, $32\% I_i$ is incident on the second filter, again 32% of this natural light is transmitted so we have 32%(32% I_i). Now if this is unpolarized light, do we need to add this to the percentage of polarized light incident on the second filter? And does each filter polarize half of the incoming flux density?

 

[TSny]

The attached picture shows the setup. There's a difference in what goes on at each filter. The first filter has unpolarized light ("natural light") incident on it. By definition, an HN-32 filter will reduce the intensity of the unpolarized light to 32% of the incident intensity of the unpolarized light. And it will convert the unpolarized light to polarized light.

But the second filter has polarized light incident on it rather than unpolarized light. Also, the direction of polarization of the incident light is the same direction as the transmission axis of the second filter. If the second filter were an ideal polarizer rather than an HN-32 filter, it would allow 100% of the incident polarized light to pass. (Such an ideal polarizer would be an HN-50 filter since it would let 50% of unpolarized light pass through.) Anyway, since the incident light is already polarized in the transmission axis direction of the second HN-32 filter, the intensity of the transmitted light will be more than 32% of the intensity of the light incident on the second filter.

 

[roam]

Thank you very much for the diagram. Frankly I've been thinking about this and unfortunately I still don't see where the "64%" comes from. Since in this case we are using HN-32 and not the hypothetical ideal HN-50, an intensity of 32%I_i is incident on the second polarizer as in the diagram. And as you said this light is already polarized in the same orientation as the transmission axis of the second filter. So its intensity should not be decreased further by another 32%. How do I know exactly what percentage of this light goes past the second filter? How do we get 64%?

 

[TSny]

Suppose we have an ideal polarizer (HN-50). If polarized light of intensity I_o is incident on the filter, the intensity that gets through is given by Malus' law I = I_ocos²(θ) where θ is the angle between the polarization direction and the transmission axis of the filter.

Unpolarized light has a polarization that jumps randomly over all angles θ, so the intensity that gets through is obtained by averaging Malus' law over all angles:

I = I_o<cos²θ> = I_o$\cdot$$\frac{1}{2}$ because the average of the square of the cosine function is 1/2. So, an ideal filter let's 50% of "natural light" through (thus, the 50 in "HN-50").

For a non-ideal polarizer, less light will get through due to reflection and maybe other effects. To take this into account we could modify Malus' law as I = eI_ocos²(θ) where e is some number less than 1.

Knowing that an HN-32 filter reduces the intensity of unpolarized light to 32% of I_o, what would be the value of e for this type of filter?

Once you have the value of e, you can use the modified Malus' law to find the intensity that is transmitted for polarized light incident on the filter an any angle θ.

 

[roam]

I solved for e as follows:

$32 \% I_0 = e \ I_0 \frac{1}{2} \implies e= 64 \%$

Is that correct?

The irradiance leaving the first linear polarizer is 32%I₀. So we can now use the modified Malus's law with cos θ=1 (since θ is the angle between the transmission axes of the analyzer and polarizer which is zero in this case):

$I=e.I_o = 64\%(32\% I_0)$

My answer is now correct, and hopefully my reasoning is also correct. Thank you so much for your help. I really do appreciate it.

 

[TSny]

Looks good!