Polarized Light Problem

[NZBRU]

I am having problems completing the following questions:

a) The answer is apparently in the -y direction (I understand that the direction of propagation is the cross product of the electric and magnetic field that must be perpendicular to each other). I am not sure how to come to this conclusion.

I am not exactly sure what direction the magnetic component is. It is denoted Bx and is in the general form of a sinusoidal wave [A sin (wt+phi)] meaning that the phase shift must be ky, where k = 2pi/λ (so k is the 'wave-number') and y is the current direction along the y-axis. The angular frequency is simply equal to 2*10^15s and the peak amplitude is 4uT.

I would assume seeing as it is denoted as Bx the magnetic field will be in the positive x direction. As it is dependent on the y-position can it be stated that the electric field is in the y direction? I am not sure how the conclusion was drawn that it is propagating in the -y direction ie B cross E is = -y

b) Seeing as it is known that B is along the x-axis and the wave is propagating along the negative y-axis it must be polarized along the z axis (as x cross z = -y which makes sense)

c) Using

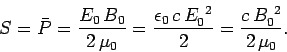
where Eo and Bo are the peak amplitudes of the electric and magnetic oscillatory fields the intensity can be found.

Bo is known to be 4uT. Uo is known (constant) to be 4pi*10^-7 (vacuum permeability) and c is known so S can be calculated to be:

592.176 W/m^2

d) General form of E

E = Eo sin (kx + wt)

Assume that the angular frequency should be equal so that wt = 2*10^-15t. The angular wave number, k, is equal to 2pi/λ. I would assume it is equal in magnitude to the magnetic field but in the x direction.

so E = Eo sin (kx + 2*10^15t)

Not sure how Eo is determined, maybe Maxwell's equations?

e) For light, f = 2*10^15/2pi, v = c so

λ = c/f = 94.247 um

f) Infared, using:

_____________________________________

That is my attempt, I am not 100% certain on many of the questions. Any help would be appreciated. Cheers.

 

[Chandra Prayaga]

Is this a homework question?

 

[BvU]

a) The answer is apparently in the -y direction

Sit at y = 0, t=0 so that $B_x = 0$ and take a time step $\Delta t$. Where do you have to go to be at the point where $B_x = 0$ again ?

(I understand that the direction of propagation is the cross product of the electric and magnetic field that must be perpendicular to each other). I am not sure how to come to this conclusion.

So far the exercise only has mentioned a B field !

 

[Chandra Prayaga]

The direction of the magnetic field is not clear. Merely calling it B_x does not make it a vector in the x-direction. You have to give a unit vector in the appropriate direction. Once that is specified, the magnetic field is in that direction.
The ky in the oscillatory part states that the propagation is in the y direction. Whether it is +y or -y is decided by the answer to BvU's question above. Once that is decided, the direction of the electric field can be given following Maxwell.

 

[BvU]

I think the OP can safely assume the exercise is about a $\vec B$ field in the x-direction.

 

[Chandra Prayaga]

Agreed.

 

[Chandra Prayaga]

Can you get E₀ from the intensity?