Poles of the self-energy in atoms and molecules

[Lebnm]

We can use the method of the Green functions to calculate ioniation potentials and electron affinities of atoms and molecules. These quantities can be determined if we know the self-energy $\Sigma(E)$, that is a function of the energy $E$. A matrix element of the self-energy in the basis of spin-orbitals has a spectral form $$\Sigma_{pq}(E) = \Sigma_{pq}(\infty) + \sum_{\mu}\frac{f_{pq\mu}}{E - M_{\mu} + i\eta} + \sum_{\nu}\frac{g_{pq\nu}}{E - N_{\nu} - i\eta},$$where $\Sigma_{pq}(\infty)$ is a E-independent term and $\eta$ is an infinitesimal positive. We can see that the self-energy has poles in the sets $\{M_{\mu}\}$ and $\{N_{\nu}\}$, but this poles are separeted by a interval $E = E_{0}$. It means that there aren't poles of the first sum between two poles of the second sum, and vice-versa. If we call the poles of the first sum by $\Sigma_{+1},\ \Sigma_{+2},\ ...$ in the increasing order and the poles of the second sum in decreasing order by $\Sigma_{-1},\ \Sigma_{-2},\ ...$, and plot a graph of the self-energy, we espect that it has a form like:

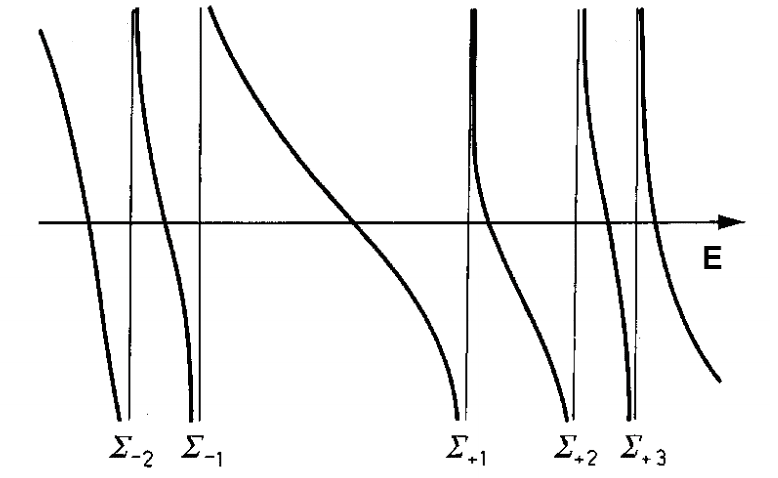
The article I am reading say that, to a closed-shell system, the interval between the poles $\Sigma_{-1}$ and $\Sigma_{+1}$ conteim the energies of the outer valence electrons. He say that is easy to see looking to the perturbation expansion of the self-energy, that is similar to the expansion of the Green function using Feynman diagrams, but I can't see why. Does anyone have any idea?

 

[eljose79]

I would like to offer some insight into the concept of using Green functions to calculate ionization potentials and electron affinities.

Firstly, the concept of Green functions is a powerful tool in quantum mechanics for solving problems involving interacting systems. It is essentially a mathematical function that describes the response of a system to a perturbation.

In the case of ionization potentials and electron affinities, the self-energy $\Sigma(E)$ is a key quantity that can be calculated using Green functions. As mentioned in the forum post, the self-energy is a function of energy $E$ and has poles at specific energies $M_{\mu}$ and $N_{\nu}$. These poles represent the energy levels of the system.

Now, for a closed-shell system, the outer valence electrons are the ones that are most easily ionized or attached by an external electric field. This means that the energies of these electrons are located in the interval between the poles $\Sigma_{-1}$ and $\Sigma_{+1}$.

To see why this is the case, we can look at the perturbation expansion of the self-energy. This expansion is similar to the expansion of the Green function using Feynman diagrams, as mentioned in the forum post.

The perturbation expansion of the self-energy involves summing over all possible excited states of the system. However, for a closed-shell system, the outer valence electrons are the only ones that can be easily excited. This means that the perturbation expansion will only involve terms that correspond to the outer valence electrons, and hence the energies of these electrons will be contained in the interval between the poles $\Sigma_{-1}$ and $\Sigma_{+1}$.

In conclusion, the use of Green functions and the concept of self-energy allows us to calculate the ionization potentials and electron affinities of atoms and molecules. And for a closed-shell system, the energies of the outer valence electrons can be easily identified by looking at the interval between the poles of the self-energy.