Polynomial Rings, UFDs and Fields of Fractions

[Math Amateur]

[This item has also been simultaneously posted on MHF]

Polynomial Rings, UFDs and Fields of Fractions

In Dummit and Foote Section 9.3 Polynomial Rings that are Unique Factorization Domains, Corollary 6, reads as follows:

================================================== ==========================
Corollary 6

Let R be a UFD, let F be its field of fractions and let

.

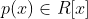Suppose the gcd the of the coefficients of p(x) is 1.

Then p(x) is irreducible in R[x] if and only if it is irreducible in F[x].

In particular, if p(x) is a monic polynomial that is irreducible in R[x], then p(x) is irreducible in F[x].

================================================== ===========================

The proof reads as follows:

================================================== ===========================

Proof:

By Gauss' Lemma, if p(x) is reducible in F[x] then p(x) is reducible in R[x].

Conversely, the assumption that gcd the of the coefficients of p(x) is 1 implies that if it is reducible in R[x], then p(x) = a(x)b(x) where neither a(x) nor b(x) are constant polynomials in R[x]. This same factorization shows that p(x) reducible in F[x].

================================================== ===========================

My problems requiring clarification are as follows:

Problem 1: The Corollary talks in terms of irreducibility while the proof talks in terms of reducibility. Why is this? How is the statement of the Corollary and the proof reconciled? Can someone give a clear clarification?

Problem 2: The proof reads "the assumption that gcd the of the coefficients of p(x) is 1 implies that if it is reducible in R[x], then p(x) = a(x)b(x) where neither a(x) nor b(x) are constant polynomials in R[x]". Can someone please show rigorously and explicitly how this follows.

Peter
​

 

[jvicens]

Hello Peter,

I am happy to help clarify your questions about this corollary and its proof.

Problem 1: The corollary and the proof are talking about the same concept, but from different perspectives. The corollary states that if a polynomial is irreducible in R[x], then it is also irreducible in F[x]. This means that if a polynomial cannot be factored in R[x], then it also cannot be factored in F[x]. On the other hand, the proof is showing that if a polynomial can be factored in R[x], then it can also be factored in F[x]. This is essentially the same statement, just phrased in a different way.

Problem 2: The assumption that gcd of the coefficients of p(x) is 1 means that the coefficients of p(x) have no common factors other than 1. This implies that if p(x) can be factored in R[x], then it must be a product of two non-constant polynomials a(x) and b(x). If a(x) and b(x) were both constant polynomials, then their coefficients would have a common factor other than 1, which contradicts our assumption. Therefore, p(x) must be reducible in F[x] as well, since it can be factored into non-constant polynomials a(x) and b(x) with coefficients in F.

I hope this helps to clarify the corollary and its proof. Let me know if you have any further questions.