- #1
Erbil
- 57
- 0
Hi.I'd like to ask a question about polynomal equations.
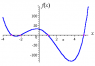
http://www.intmath.com/equations-of-higher-degree/1-polynomial-functions.php here is the solution polynomial function of degree 4. graphically.But I don't understand the method ? How we can use graphic method to solve? or can we use?
for example ; x^3+6x^2+15x+18
Can we solve this withous using the factorisation method.
http://www.intmath.com/equations-of-higher-degree/1-polynomial-functions.php here is the solution polynomial function of degree 4. graphically.But I don't understand the method ? How we can use graphic method to solve? or can we use?
for example ; x^3+6x^2+15x+18
Can we solve this withous using the factorisation method.