- #1
Russ Edmonds
- 17
- 16
- TL;DR Summary
- Net power absorbed and a tentative B vs H plot for an unloaded microwave oven transformer (MOT)
A DI-149 data acquisition module was used to record a microwave oven transformer (MOT) primary voltage and current time histories. The secondary of the MOT was open. The DI-149 analog input specs are: +- 10 volts full scale, 5000 samples per second for each channel (assuming two channels being recorded) and a ten bit ADC. One second of data was was recorded for 90v, 100v, 110v and 120v rms.The setup.

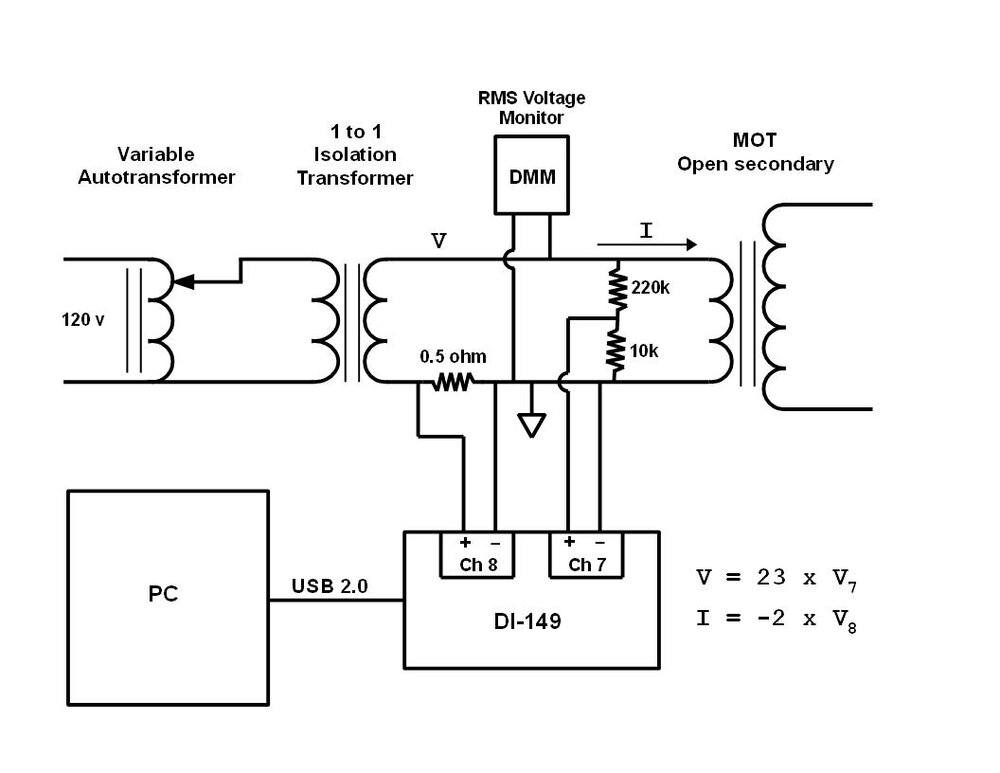
Note: The MOT HV cap is not in the circuit. One terminal of this cap is being used as a connection point for the blade/push on connectors.
Schematic of the setup.
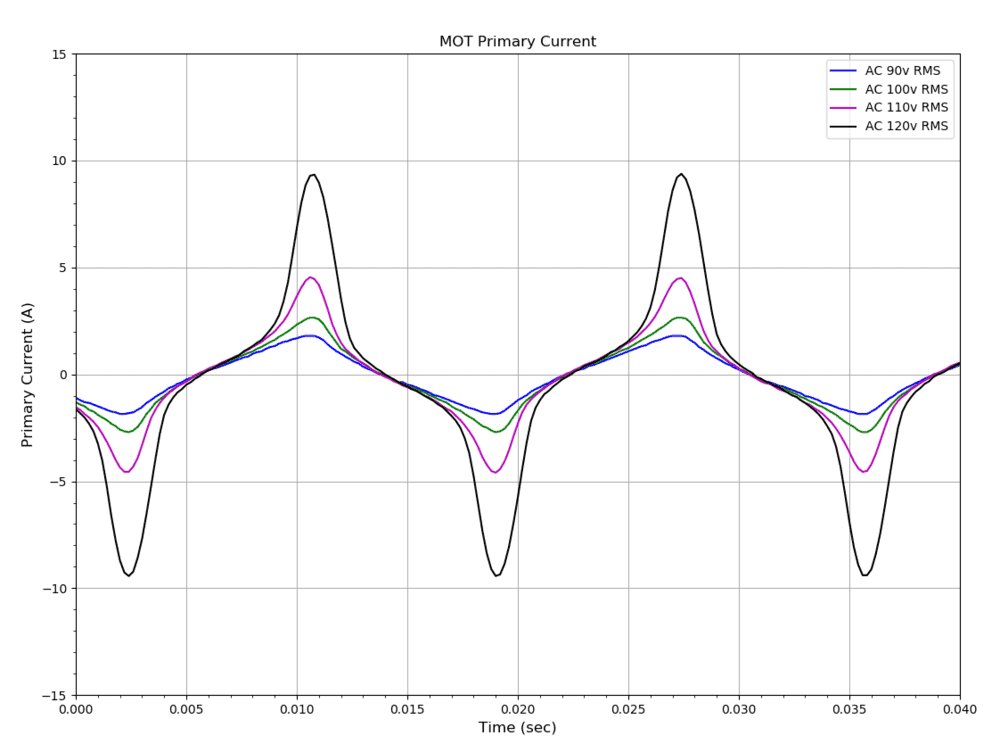
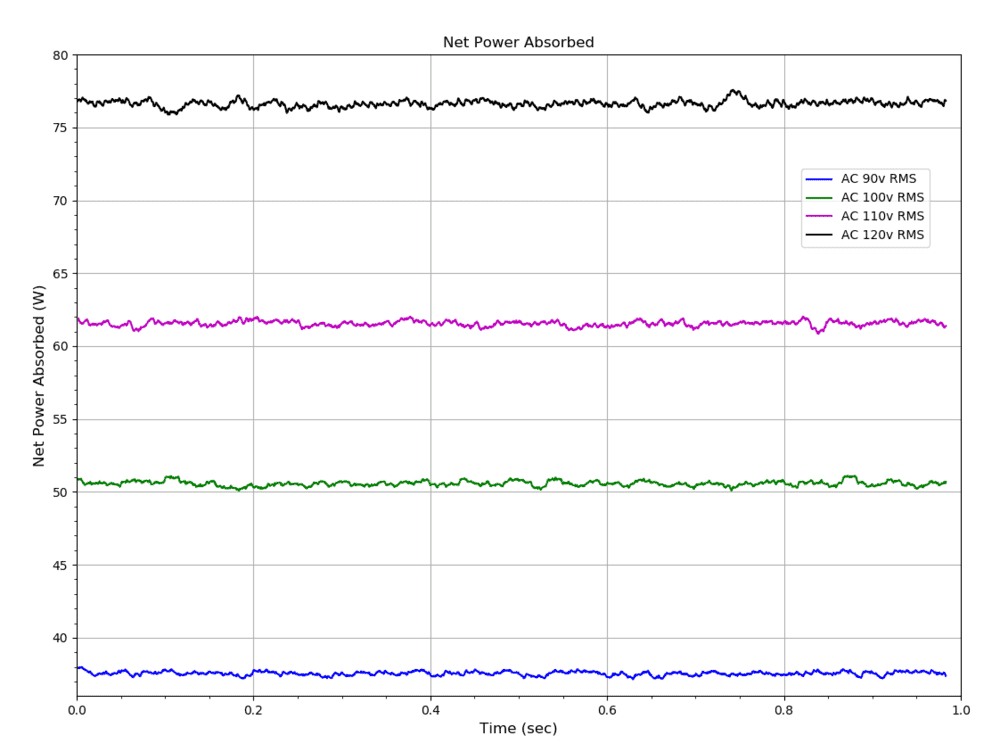
The power absorbed by the MOT at time t is given by V(t)I(t) where V(t) and I(t) are the real voltage and current at time t. The current lags the voltage by nearly 90 degrees so this term shows that the MOT alternatively absorbs and emits power. The time integral of V(t)I(t) over one period of the AC cycle (T) gives the net energy absorbed by the MOT in one T. Dividing the net energy by T then gives the net power absorbed.
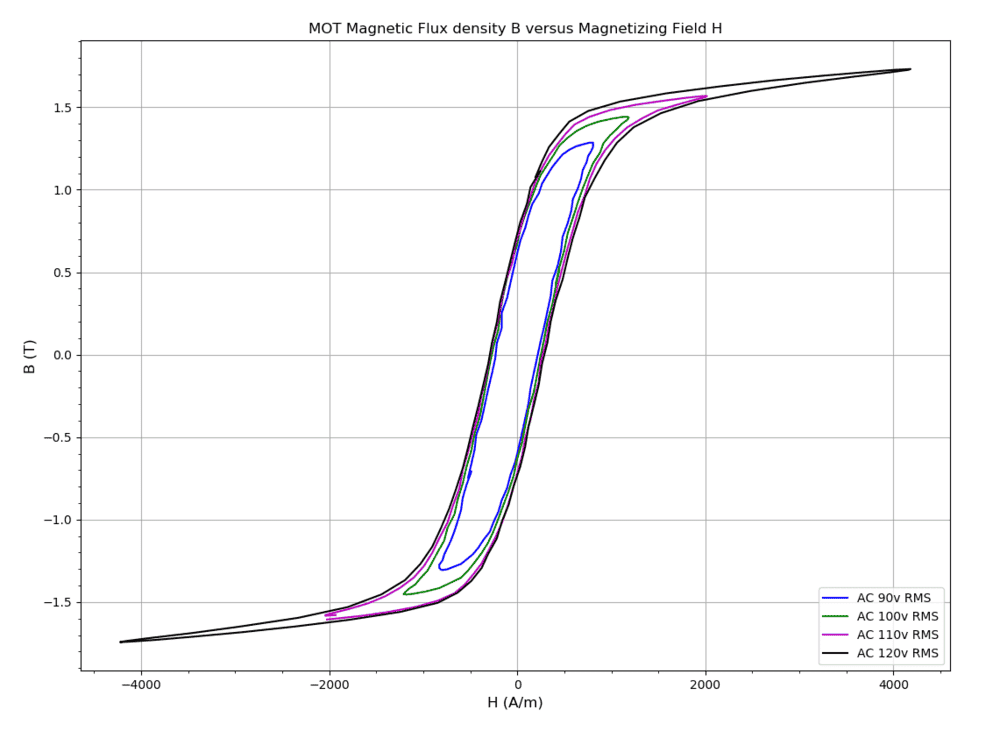
Magnetic flux density in the core is given by the time integral of voltage divided by the number of primary turns and cross sectional area of the core at the primary winding. There can also be a constant flux and flux density term in the core but this term is generally set to zero in making B vs H plots. In getting the value of the magnetizing field H, I assumed a constant H around a intermediate closed path in the core. This is probably not very accurate, also the effects of the magnetic shunts were ignored.
A tentative B vs H plot.
Note: The MOT HV cap is not in the circuit. One terminal of this cap is being used as a connection point for the blade/push on connectors.
Schematic of the setup.
The power absorbed by the MOT at time t is given by V(t)I(t) where V(t) and I(t) are the real voltage and current at time t. The current lags the voltage by nearly 90 degrees so this term shows that the MOT alternatively absorbs and emits power. The time integral of V(t)I(t) over one period of the AC cycle (T) gives the net energy absorbed by the MOT in one T. Dividing the net energy by T then gives the net power absorbed.
Magnetic flux density in the core is given by the time integral of voltage divided by the number of primary turns and cross sectional area of the core at the primary winding. There can also be a constant flux and flux density term in the core but this term is generally set to zero in making B vs H plots. In getting the value of the magnetizing field H, I assumed a constant H around a intermediate closed path in the core. This is probably not very accurate, also the effects of the magnetic shunts were ignored.
A tentative B vs H plot.