Exploring Pressure at Different Depths: A Puzzling Concept

[Hereformore]

I'm having some trouble reconciling different concepts when it comes to pressure.

I know that:
1) Pressure in a container or in any fluid in a closed container depends on depth by P=Patm + pgd.

2) Pressure is felt on all sides of an object.

So if you have a cube in tank of water, then the cube should feel pressure on all of its sides.

The forces and pressure on the non -top and bottom sides should cancel out because they are equal and opposite each other.

The forces on the top and bottom of the cube, however, do not cancel out because they are at different heights.
The top of the cube should feel a lower pressure than the bottom of the cube, right?

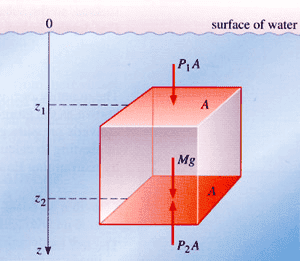
The difference in pressure will equal the difference in depth so: Pbottom-Ptop = pg(Depth at Bottom - Depth at Top of Cube).

So if you have a cube that is submeged in water as shown above, and if it is not moving up or down (so its still, all forces cancel), we have the forces:

Fy = Fw - Fbouyancy = 0 N

For Pressure we have: P Bottom > Ptop from the water. What other component am I missing? If the pressure from the bottom is larger than the pressure pushing down from the top, then the object should be moving up shouldn't it? Or am I misunderstanding pressure at different depths completely.

This leads to my followup question: we know pressure at lower depths is greater, but that means that at lower depths you feel a greater force and pressure. But intuitively you would think that at lower depths the pressure would be greater downards weighing down upon you wouldn't you?
But for floating objects, although the presure is greater, it points up?

Edit: Oh wait! Is it actually kind of like the water is pushing back up against the bottom of the cube? Or is it something else entirely? I can't wrap my head around the greater pressure at a lower depth pointing opposite the very mass/liquid that gives it its greater pressure.

 

[russ_watters]

Pressure is a scalar: at any specific point, it acts in all directions, equally. It doesn't "point" up or down.

 

[Hereformore]

Pressure is a scalar: at any specific point, it acts in all directions, equally. It doesn't "point" up or down.

I see. SO is the depth relationship just a convenient way to quantify its magnitude? my trouble is that in attaching an intuitive explanation to it (deeper = more water above you to push down upon you) i can't relate it back to why pressure would point up.

If it's not the amount of substance "above you" (qualitatively speaking) then what about the depth makes pressure greater? Because if it were purely about how much is above you then it sholdnt point up as well you know?

 

[ModusPwnd]

The pressure doesn't point up. But the net force on the object does (or can, maybe it points down). You need to relate the pressure at a point to the area of the object to get a force. You need to sum those forces and equate to "ma" to get a picture of what will happen to the object.

 

[Dale]

i can't relate it back to why pressure would point up.

Pressure doesn't point up. Pressure is a scalar, so it doesn't have a direction.

The thing that has a direction is the buoyant force, which is pressure times area. The area is what contributes the direction, not the pressure. Specifically, the direction of the buoyant force is the direction normal to the surface.

So the net buoyant force points up because the normal vector to the bottom is up and that is where the directionless pressure is greatest.

 

[Hereformore]

Pressure doesn't point up. Pressure is a scalar, so it doesn't have a direction.

The thing that has a direction is the buoyant force, which is pressure times area. The area is what contributes the direction, not the pressure. Specifically, the direction of the buoyant force is the direction normal to the surface.

So the net buoyant force points up because the normal vector to the bottom is up and that is where the directionless pressure is greatest.

I see! That makes a lot more sense.

So it is a common (or maybe just me) misconception that pressure points down, maybe due to water pressure when you imagine being at the bototm of the sea. But the reality is that it doesn't have direction and the force determines the direction.

And the magnitude is determined by the depth?

 

[Chestermiller]

Pressure is a scalar only in the same sense that the magnitude of a vector is a scalar. In more advanced treatments of fluid dynamics, the directional character of pressure is captured mathematically by recognizing that it represents the magnitude of the isotropic portion of the mechanical (second order) stress tensor. For an Euler fluid, for example, the stress tensor is expressed mathematically as:
$$\vec{\sigma}=-p\vec{I}$$
where we employ the convention that tensile stresses are positive, and where $\vec{I}$ represents the identity tensor. In Cartesian component form, using dyadic notation, the identity tensor is given by:
$$\vec{I}=\vec{i}_x\vec{i}_x+\vec{i}_y\vec{i}_y+\vec{i}_z\vec{i}_z$$
The Cauchy Stress Relationship is used to determine the traction vector (aka stress vector) acting on a differential element of area present within the fluid whose unit normal is $\vec{n}$:
$$\vec{\tau}=\vec{\sigma}\centerdot\vec{n}$$
The traction vector $\vec{\tau}$ represents the vector force per unit area exerted by the fluid on the side of the differential element of area toward which $\vec{n}$ is directed and acting on the fluid on the side of the differential element of area from which $\vec{n}$ is directed.
In the example of our little cube, the traction stress on a surface oriented normal to the x direction is obtained by dotting the stress tensor with $\vec{n}=\vec{i}_x$ to yield: $$\vec{\tau}=\vec{\sigma}\centerdot\vec{i}_x=-p\vec{i}_x$$. Similarly, for a surface oriented normal to the z direction, $$\vec{\tau}=\vec{\sigma}\centerdot\vec{i}_z=-p\vec{i}_z$$. This is how the isotropic nature of pressure is captured mathematically in advanced fluid mechanics treatments.

I might also comment that the same issue of directionality arises in ordinary mechanics with respect to the tension in a wire. The stress tensor within the wire is given by:
$$\vec{\sigma}=\frac{T}{A}\vec{i}_x\vec{i}_x$$
where T is the magnitude of the tension (a scalar), A is the cross sectional area, and $\vec{i}_x$ is a unit vector along the wire. The same approach is used to determine the tension force (vector) exerted by one portion of the wire on an adjacent portion of the wire across a given cross sectional area A.

Chet

 

[sophiecentaur]

http://www.science2education.co.uk/product/PH0194 of hydrostatic pressure acting equally in all directions. It consists of a clear plastic cylinder with a plastic ball at the end. Holes are drilled all over the surface of the sphere. You fill the thing with water by withdrawing the piston and then 'squish' out the water by pushing the piston briskly. Water squirts out of the holes, in all directions with, convincingly, the same force / velocity from each. It is an entertaining teaching aid but is best done outside . . . . .

The 'direction' of the hydrostatic pressure in the fluid, at depth, is meaningless but, when you put an object in the fluid, the pressure acts against the surface, all over the object and there is a direction to the force. (I think that could be a partial translation of Chet's post, above) So the parts of the object facing 'down' will have an overall upward component of pressure and there is a corresponding downward pressure component for all upward facing parts. This difference is what generates the upthrust. (All pretty obvious)
But there is another issue and that is the reason for why objects always float with a certain orientation (e.g. a stick always floats on its side. This is because of the Potential Energy of the object. Pushing the end of a stick further under water will increase the PE because you are doing Work when you try to rotate it. The horizontal position ( or whatever - depending on the the object's shape and mass distribution) has minimal PE. There will be the same upthrust for all positions - if you put the stick in a vertical tube of water, the same fraction of the stick will still be above water when it's in equilibrium as when it's on its side.

 

[Chestermiller]

when you put an object in the fluid, the pressure acts against the surface, all over the object and there is a direction to the force. (I think that could be a partial translation of Chet's post, above)

Yes. This is one of the things the mathematics I presented captures.

Chet

 

[Dale]

Also, the math you posted works for solids, where there are shear stresses.

 

[Chestermiller]

Also, the math you posted works for solids, where there are shear stresses.

Yes. I was just trying to keep things as simple as I could.

Chet

 

[sophiecentaur]

Yes. This is one of the things the mathematics I presented captures.

Chet

. . . . I though it did but it's not at my level, these days.

 

[Chestermiller]

Also, the math you posted works for solids, where there are shear stresses.

Newtonian fluids also exhibit shear stresses when they are deforming with respect to time.

Chet