- #1
xzibition8612
- 142
- 0
Homework Statement
See attachment.
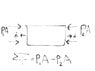
The net pressure force on this control volume is P1*A - P2*A. My question concerns the direction signs.
My thinking is this:
The unit vector on the control volume naturally points outward (n hat). Since the pressure force PA is pushing TOWARDS the control volume, dotting PA and (n hat) would give you -PAn (since the force and unit vector are in opposite directions). Summing the pressure force on this control volume should then yield -P1A-P2A. So I'm very confused why the correct answer is P1A-P2A. Thanks. Maybe I screwed up on the unit vector, is it different for pressure?
Homework Equations
The Attempt at a Solution
Attachments
Last edited: