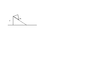- #1
JohanL
- 158
- 0
If you have two prisms on top of each other, one smaller than the other, and the one on top glids down to the ground the lower prisms moves to the left.
The problem is to find how far the lower prism moves.
How do you set up the Lagrangian and the constraints for this problem?
Any ideas?
The problem is to find how far the lower prism moves.
How do you set up the Lagrangian and the constraints for this problem?
Any ideas?