- #1
indifferent_2
- 5
- 0
I have a quiz and I don't know how to solve this question ? Help me
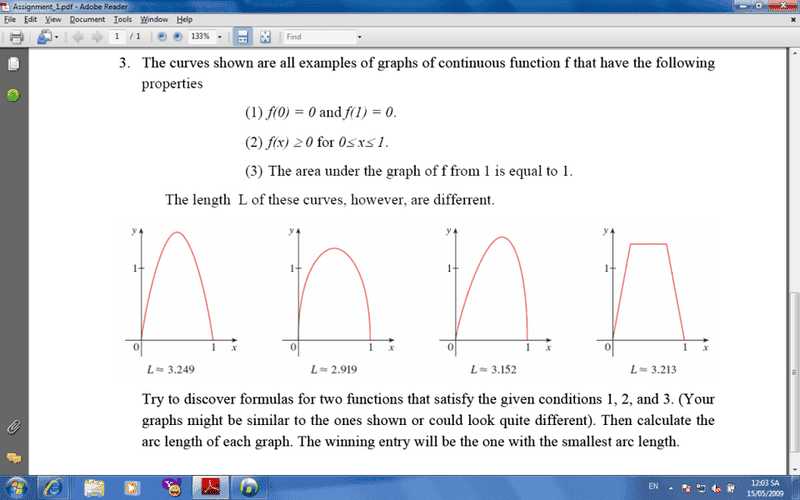
This is my first post . I don't know where to post this topic . Can you move this topic into right place , Mod ?
This is my first post . I don't know where to post this topic . Can you move this topic into right place , Mod ?