- #1
stunner5000pt
- 1,461
- 2
look at the figure in the attachment
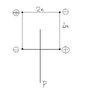
The black dots at the ends of the square in the figure represent charges -q or +q and they are denoted + or - by the symbol next to the them.
Now that line is drawn from the centre of the square to point P and is distance x
The side of the square is 2a
Show that Electric Field at P for x >> a is 3 (2qa^2) / 2 pi epsilon0 x^4
so far i came up with this
for the dipole closer to P the expression would be
E = (1/4 pi epsilon) 2qa/ [(x-a)^2 +(2a/2)^2]^3/2
and after a lot of algebra i get
E = (qa / 2 pi epsilon ) * 1 / [ x^2 + 2xa + 2a^2]^3/2
for the first closer dipole
for the more distant dipole i get E = - (1/4 pi epsilon) 2qa / [ (x+a)^2 + a^2 ] ^3/2
more algebra i get E = - (qa / 2 pi epsilon ) * 1 / [x^2 + 2xa + 2a^2]^3/2
but it is after this point that i am stuck completely
how do i get to the expression that is needed??
please please help!
The black dots at the ends of the square in the figure represent charges -q or +q and they are denoted + or - by the symbol next to the them.
Now that line is drawn from the centre of the square to point P and is distance x
The side of the square is 2a
Show that Electric Field at P for x >> a is 3 (2qa^2) / 2 pi epsilon0 x^4
so far i came up with this
for the dipole closer to P the expression would be
E = (1/4 pi epsilon) 2qa/ [(x-a)^2 +(2a/2)^2]^3/2
and after a lot of algebra i get
E = (qa / 2 pi epsilon ) * 1 / [ x^2 + 2xa + 2a^2]^3/2
for the first closer dipole
for the more distant dipole i get E = - (1/4 pi epsilon) 2qa / [ (x+a)^2 + a^2 ] ^3/2
more algebra i get E = - (qa / 2 pi epsilon ) * 1 / [x^2 + 2xa + 2a^2]^3/2
but it is after this point that i am stuck completely
how do i get to the expression that is needed??
please please help!
Attachments
Last edited: