- #1
blaziken's_charizard
- 34
- 0
1. A boy can throw a stone at 14 m/s. At what angle must he throw it in order to hit a window which is 10m away horizontally and 5m above the ground?
2. I would assume we have to use trig ratios and the kinematics equations.
v = u + a.t
v^2 = u^2 + 2.a.s
s = u.t + 1/2.a.t^2
3. Diagram:
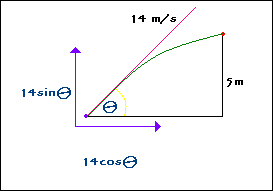
(see attachment or http://img377.imageshack.us/my.php?image=imgwn9.png )I know that time is a constant for both the horizontal and vertical components, so I presume that it would not affect the equations.
My info:
-Vertical motion
(t=0)
s = 5m
u = 14 m/s sin.(theta)
a = +9.8 m/s^2
-Horizontal motion
(t=0)
s = 10m
u = 14 m/s cos.(theta)
a= 0
So how do I find theta? Am I missing any equations? Is my diagram correct? Is u = 14 m/s sin.(theta) and u = 14 m/s cos.(theta) correct? Thanks :)
I'm thinking of using some equation in theta... but what those equations are is beyond me =[
2. I would assume we have to use trig ratios and the kinematics equations.
v = u + a.t
v^2 = u^2 + 2.a.s
s = u.t + 1/2.a.t^2
3. Diagram:
(see attachment or http://img377.imageshack.us/my.php?image=imgwn9.png )I know that time is a constant for both the horizontal and vertical components, so I presume that it would not affect the equations.
My info:
-Vertical motion
(t=0)
s = 5m
u = 14 m/s sin.(theta)
a = +9.8 m/s^2
-Horizontal motion
(t=0)
s = 10m
u = 14 m/s cos.(theta)
a= 0
So how do I find theta? Am I missing any equations? Is my diagram correct? Is u = 14 m/s sin.(theta) and u = 14 m/s cos.(theta) correct? Thanks :)
I'm thinking of using some equation in theta... but what those equations are is beyond me =[
Last edited: