- #1
Gyro
- 49
- 0
Could someone please check my work and provide insight on what I may be missing to complete the problem.
The question's from Ray Serway's Physics For Scientists & Engineers 4th Ed. Vol. 1. Chapter 4. Review Problem #1. Page 95.
A ball is thrown with an initial speed [tex]v_0[/tex] at an angle [tex]\theta_0[/tex] with the horizontal. The range of the ball is [tex]R[/tex]
and the ball reaches a maximum height of [tex]R/6[/tex]. In terms of [tex]R[/tex] and [tex]g[/tex], find
a) the time the ball is in motion,
b) the ball's speed at the peak of its path,
c) the initial vertical component of its velocity,
d) its initial speed,
e) the angle [tex]\theta_0[/tex],
f) the maximum height that can be reached if the ball is thrown at the appropriate angle and at the speed found in d),
g) the maximum range that can be reached if the ball is thrown at the appropriate angle and at the speed found in d).
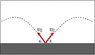
h) Suppose two rocks are thrown from the same point at the same moment as shown in the figure. Find the distance between them as a function of time. Assume [tex]v_0[/tex] and [tex]\theta_0[/tex] are given.
2. Homework Equations
[tex]y_{peak} = R/6[/tex]
[tex]y = v_0_yt - 1/2gt^2 = R/6------>(1)[/tex]
[tex]v_y_{peak} = 0 = v_0_y - gt ==>v_0_y = gt-->(2)[/tex]
[tex] (2) -> (1): R/6 = (gt)t - 1/2gt^2 = 1/2gt^2[/tex]
[tex]t = \sqrt\frac{R}{3g}[/tex]
Quickly checking dimensions,
[tex]\sqrt\frac{L}{LT^-2} = T[/tex]
a) The time of flight is twice the time it takes to get to its peak.
[tex]T_{total} = 2t = \sqrt\frac{4R}{3g}[/tex]
b) At the ball's peak [tex]v_y = 0[/tex], so the speed is all horizontal.
We also know that at its peak, the ball has traveled half its range.
[tex]R/2 = v_0_xt[/tex]
[tex]v_0_x = \frac{R}{2\sqrt\frac{R}{3g}} = \frac{R}{2} * \sqrt\frac{3g}{R} = \sqrt\frac{3Rg}{4}[/tex]
Quickly checking dimensions,
[tex]\sqrt(L*LT^-2) = LT^-1[/tex]
c)
[tex](2): v_0_y = gt = g\sqrt\frac{R}{3g} = \sqrt\frac{Rg}{3}[/tex]
Quickly checking dimensions,
[tex]\sqrt(L*LT^-2) = LT^-1[/tex]
d)
[tex]v_0 = \sqrt(v_0_x^2 + v_0_y^2)[/tex]
[tex]= \sqrt(3/4Rg + 1/3Rg) = \sqrt(\frac{9Rg + 4Rg}{12}) = \sqrt(13/12Rg)[/tex]
e)
[tex]\tan\theta = \frac{v_0_y}{v_0_x} = \frac{\sqrt(\frac{Rg}{3})}{\sqrt(\frac{3Rg}{4})} = \sqrt\frac{Rg}{3}*\sqrt\frac{4}{3Rg} = \sqrt\frac{4}{9} = \frac{2}{3}[/tex]
[tex]\theta_0 = 33.69^o[/tex]
f) What is the question asking, exactly? By the way the question is worded, it sounds like they're asking what max height can the ball reach given the initial speed found above. That happens when the ball is thrown straight up. In that case [tex]\theta_0 = 90^o[/tex]
Projectile Height Eq'n:
[tex] y_{max} = \frac{v_0^2\sin^2\theta_0}{2g}[/tex]
[tex] = \frac{(13/12Rg)(\sin^2(90^o))}{2g} = (\frac{13Rg}{12}*\frac{1}{2g}) = \frac{13R}{24}[/tex]
How do I interpret that answer? Does it say the ball would vertically travel (13/24*100 =) 54.2% of the Range it would travel horizontally if it is thrown with the same speed but at an angle of [tex]33.69^o[/tex] instead?
g) The maximum range occurs when [tex]\theta_0 = 45^o[/tex]
Projectile Range Eq'n:
[tex] x_{max} = \frac{v_0^2\sin2\theta_0}{g} = \frac{(13/12Rg)(\sin90^o)}{g} = \frac{13/12Rg}{g} = \frac{13R}{12}[/tex]
This makes some sense to me. If the ball were thrown at [tex]45^o[/tex] rather than [tex]33.69^o[/tex], it would horizontally travel farther by 1/12R.
h) My thinking here is that since the rocks take mirrored projectile paths, the distance between them will always be a horizontal line, the length being twice the horizontal distance of one rock from the origin.
[tex] D = 2*v_0\cos\theta_0 *t [/tex]
That seems too a simple an answer. Am I missing something?
All help appreciated.
Thanks in advance.
EDIT: Maybe this question should be in the Intro category. Sorry if so.
The question's from Ray Serway's Physics For Scientists & Engineers 4th Ed. Vol. 1. Chapter 4. Review Problem #1. Page 95.
Homework Statement
A ball is thrown with an initial speed [tex]v_0[/tex] at an angle [tex]\theta_0[/tex] with the horizontal. The range of the ball is [tex]R[/tex]
and the ball reaches a maximum height of [tex]R/6[/tex]. In terms of [tex]R[/tex] and [tex]g[/tex], find
a) the time the ball is in motion,
b) the ball's speed at the peak of its path,
c) the initial vertical component of its velocity,
d) its initial speed,
e) the angle [tex]\theta_0[/tex],
f) the maximum height that can be reached if the ball is thrown at the appropriate angle and at the speed found in d),
g) the maximum range that can be reached if the ball is thrown at the appropriate angle and at the speed found in d).
h) Suppose two rocks are thrown from the same point at the same moment as shown in the figure. Find the distance between them as a function of time. Assume [tex]v_0[/tex] and [tex]\theta_0[/tex] are given.
2. Homework Equations
[tex]y_{peak} = R/6[/tex]
The Attempt at a Solution
[tex]y = v_0_yt - 1/2gt^2 = R/6------>(1)[/tex]
[tex]v_y_{peak} = 0 = v_0_y - gt ==>v_0_y = gt-->(2)[/tex]
[tex] (2) -> (1): R/6 = (gt)t - 1/2gt^2 = 1/2gt^2[/tex]
[tex]t = \sqrt\frac{R}{3g}[/tex]
Quickly checking dimensions,
[tex]\sqrt\frac{L}{LT^-2} = T[/tex]
a) The time of flight is twice the time it takes to get to its peak.
[tex]T_{total} = 2t = \sqrt\frac{4R}{3g}[/tex]
b) At the ball's peak [tex]v_y = 0[/tex], so the speed is all horizontal.
We also know that at its peak, the ball has traveled half its range.
[tex]R/2 = v_0_xt[/tex]
[tex]v_0_x = \frac{R}{2\sqrt\frac{R}{3g}} = \frac{R}{2} * \sqrt\frac{3g}{R} = \sqrt\frac{3Rg}{4}[/tex]
Quickly checking dimensions,
[tex]\sqrt(L*LT^-2) = LT^-1[/tex]
c)
[tex](2): v_0_y = gt = g\sqrt\frac{R}{3g} = \sqrt\frac{Rg}{3}[/tex]
Quickly checking dimensions,
[tex]\sqrt(L*LT^-2) = LT^-1[/tex]
d)
[tex]v_0 = \sqrt(v_0_x^2 + v_0_y^2)[/tex]
[tex]= \sqrt(3/4Rg + 1/3Rg) = \sqrt(\frac{9Rg + 4Rg}{12}) = \sqrt(13/12Rg)[/tex]
e)
[tex]\tan\theta = \frac{v_0_y}{v_0_x} = \frac{\sqrt(\frac{Rg}{3})}{\sqrt(\frac{3Rg}{4})} = \sqrt\frac{Rg}{3}*\sqrt\frac{4}{3Rg} = \sqrt\frac{4}{9} = \frac{2}{3}[/tex]
[tex]\theta_0 = 33.69^o[/tex]
f) What is the question asking, exactly? By the way the question is worded, it sounds like they're asking what max height can the ball reach given the initial speed found above. That happens when the ball is thrown straight up. In that case [tex]\theta_0 = 90^o[/tex]
Projectile Height Eq'n:
[tex] y_{max} = \frac{v_0^2\sin^2\theta_0}{2g}[/tex]
[tex] = \frac{(13/12Rg)(\sin^2(90^o))}{2g} = (\frac{13Rg}{12}*\frac{1}{2g}) = \frac{13R}{24}[/tex]
How do I interpret that answer? Does it say the ball would vertically travel (13/24*100 =) 54.2% of the Range it would travel horizontally if it is thrown with the same speed but at an angle of [tex]33.69^o[/tex] instead?
g) The maximum range occurs when [tex]\theta_0 = 45^o[/tex]
Projectile Range Eq'n:
[tex] x_{max} = \frac{v_0^2\sin2\theta_0}{g} = \frac{(13/12Rg)(\sin90^o)}{g} = \frac{13/12Rg}{g} = \frac{13R}{12}[/tex]
This makes some sense to me. If the ball were thrown at [tex]45^o[/tex] rather than [tex]33.69^o[/tex], it would horizontally travel farther by 1/12R.
h) My thinking here is that since the rocks take mirrored projectile paths, the distance between them will always be a horizontal line, the length being twice the horizontal distance of one rock from the origin.
[tex] D = 2*v_0\cos\theta_0 *t [/tex]
That seems too a simple an answer. Am I missing something?
All help appreciated.
Thanks in advance.
EDIT: Maybe this question should be in the Intro category. Sorry if so.
Attachments
Last edited: