What is the proof for triangle ABC with known sides and angle relationships?

In summary, the conversation discusses a problem involving triangle ABC with given side lengths and a line CD extending towards point B. The Angle BCD is equal to angle DAC and the goal is to find the length of BD. Multiple methods are tried, including folding the triangles and using the angle bisector theorem, which states that CD/BD = AC/AB. After some difficulty, the length of BD is determined to be 1.7 units.
  • #1
Blissfulpain
ok, I'm in first year coolege and we're doing some review from high school work.. but i can't for the life of me remember how to do one of these questions and i can't seem to get past this one part or at least figure out how to prove that it is what i think it is.

it's going to be a bit trickier, because i can't insert a picture, but i guess that isn't of the most importance anyways. alright

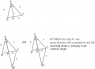
you have triangle ABC.
side AB=4 units
side AC=7 units
the line CD extends for 3 units towards point B, the distance between point B an D is unknown and is what needs to be found
the Angle BCD is = angle DAC

here's what I've tried to do so far...

i've tried to fold the 2 triangles in half across the line AD, which lines up the two sides AB and AC, with the line AC extending 3 units futher then line AB. I'm still trying to follow this train of reasoning.. but so far with little success, i don't really know what to do next, but i think it helps somehow : )

next...

I tried extending the common side between the two triangles, line AD, far enough so that i can draw a new line, 7 units long, from point C, i'll call the intersection point E. The problem arises when i can't prove that the new triangle DEC is the same as triangle ADC. I CAN prove that it is proportional to triangle ABD, but that doesn't help me, because i only know that the side CE is 7 units, the Side DC is 3 units, and i don't know if i can prove that the angle DEC is equal to the angle DAC... which means i can't prove that the line DE is a continuation of the line AD...

hence I'm lost.

thx for the help in advance.. hey, kewl... just found the attacthment thing... i'll go draw a picture and then post :)
 

Attachments

  • Triangle Diagram.png
    Triangle Diagram.png
    5.7 KB · Views: 516
Physics news on Phys.org
  • #2
Hint: angle bisector theorem.

Hope that helps!
 
  • #3
nope, doesn't help... i looked it up on the net, and got this "The angle bisector of an angle in a triangle divides the opposite side in the same ratio as the sides adjacent to the angle."

so the angle bisector is line AD, and the adjacent and opposiye side are? i can't assume ANY right angles... and all the other stuff i found on this theorem had something to do with area of a triangle, which i can't do either, because i don't have enough info to find that yet...

a bit more of a hint is needed :confused:
 
  • #4
Blissfulpain said:
nope, doesn't help... i looked it up on the net, and got this "The angle bisector of an angle in a triangle divides the opposite side in the same ratio as the sides adjacent to the angle."

so the angle bisector is line AD, and the adjacent and opposiye side are? i can't assume ANY right angles... and all the other stuff i found on this theorem had something to do with area of a triangle, which i can't do either, because i don't have enough info to find that yet...

a bit more of a hint is needed :confused:

No right angles required, merely an understanding of the words adjacent and opposite.

Let me paraphrase the theorem for the triangle you've got :

Simply, it says that CD/BD = AC/AB.

Now go back and understand what the theorem is trying to say.
 
  • #5
so, 3/x=4/7
3/x=1.75
x=1.75*3
x=5.25
huh, i had gotten that number before... just couldn't prove that it was the right number... now i can with that theorem

thx a lot guys :)))))
 
  • #6
oops... i mean 3/7=x/4
so 3/7=.429
.429x4=1.7 units

therefore BD=1.7
 

1. What is the Pythagorean Theorem?

The Pythagorean Theorem states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. In other words, a² + b² = c², where c is the length of the hypotenuse and a and b are the lengths of the other two sides.

2. How does the Pythagorean Theorem relate to triangle ABC?

Triangle ABC is not necessarily a right triangle, so the Pythagorean Theorem cannot be directly applied. However, if we know the lengths of the three sides of triangle ABC, we can use the Law of Cosines to determine the measure of any angle, including the right angle. This can then be used to prove the relationships between the sides and angles of triangle ABC.

3. What is the Law of Cosines?

The Law of Cosines is a formula that relates the lengths of the sides of a triangle to the cosine of one of its angles. It states that c² = a² + b² - 2ab*cos(C), where c is the length of the side opposite angle C, and a and b are the lengths of the other two sides.

4. How can the Law of Cosines be used to prove triangle ABC?

By knowing the lengths of the sides of triangle ABC and using the Law of Cosines, we can solve for the measure of any angle in the triangle. If we can prove that the angles and sides of the triangle are in the correct relationships based on the given information, then we can say that triangle ABC is proven.

5. Can triangle ABC be proven without using the Law of Cosines?

Yes, there are other methods that can be used to prove the relationships between the sides and angles of triangle ABC. For example, we can use the Law of Sines to determine the measures of angles based on the ratios of the sides, or we can use the properties of similar triangles to prove the relationships. However, the Law of Cosines is often the most efficient and straightforward method to use when given known sides and angle relationships.

Similar threads

B A triangle problem: Prove that |AC|+|AB|=|PR|+|PQ| given some constraints
    • General Math
Replies
13
Views
2K
MHB Difference of angles in a triangle
    • General Math
Replies
4
Views
908
MHB Find $\angle B$ for Triangle $ABC$ with Bisectors $AD,BE$
    • General Math
Replies
1
Views
757
MHB Proving Equality of Angles in an Acute Triangle
    • General Math
Replies
4
Views
765
MHB What are the angles of isosceles triangle ABC?
    • General Math
Replies
1
Views
729
I Chiral symmetries in E[SUP]^n[/SUP]
    • General Math
Replies
1
Views
994
MHB Geom Ch: Prove $AB=x^3$ Given $\triangle ABC$ & $\triangle AEF$
    • General Math
Replies
1
Views
841
MHB What are the angles of an isosceles triangle with a specific ratio?
    • General Math
Replies
2
Views
888
MHB Acute Triangle ABC: Point P and Line Intersections Formula
    • Math POTW for Secondary and High School Students
Replies
1
Views
803
MHB Barycentric coordinates in a triangle - proof
    • Linear and Abstract Algebra
Replies
5
Views
2K

Hot Threads

Recent Insights

Back
Top