- #1
heavystray
- 71
- 0
i have an equation like this:
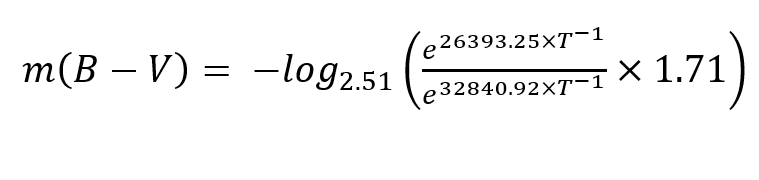
Given m(B-V)= 1.2 +- 0.2
How do you calculate the uncertainty in T? (btw, I solve T using graphs by finding the intersection point)
My idea was first to calculate T when m(B-V) =0.2, and I then calculate T when m(B-V)= 1.2 + 0.2(its uncertainty). and then find the difference between the two T. Your help would be greatly appreciated
Given m(B-V)= 1.2 +- 0.2
How do you calculate the uncertainty in T? (btw, I solve T using graphs by finding the intersection point)
My idea was first to calculate T when m(B-V) =0.2, and I then calculate T when m(B-V)= 1.2 + 0.2(its uncertainty). and then find the difference between the two T. Your help would be greatly appreciated
Attachments
Last edited: