Prove the scalar product

[Karol]

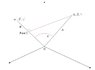
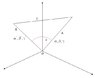
Two lines A and B. The angle between them is θ, their direction cosines are (α,β,γ) and (α',β',γ'). Prove, ON GEOMETRIC CONSIDERATIONS:
$\cos\theta=\cos\alpha\cos\alpha'+\cos\beta\cos\beta'+\cos\gamma\cos\gamma'$

I posted this question long ago and i was told that this is the scalar product and i accepted then, but now i read further in the book and they explain the scalar product but still want the geometric proof.

 

[Dr. Courtney]

What do you mean, "On GEOMETRIC CONSIDERATIONS"?

Do you mean you want a proof without using vectors?

 

[Karol]

well i don't know, i think without since i was asked at the beginning of studying vectors. the book explained the inner product and the equation i gave, but asked to prove it on geometric basis.
I was told that the cosine rule is involved but i don't know how:
$$C^2=A^2+B^2-2AB\cos\theta\;\rightarrow C^2=1+1-2\cos\theta$$
$$C^2=\cos^2\alpha+\cos^2\beta+\cos^2\gamma+\cos^2\alpha'+\cos^2\beta'+\cos^2\gamma'-2\cos\theta$$

 

[tommyxu3]

If you regarded $A,B$ as two unit vectors, then their scalar product would be what you write.
For $$A\cdot B=|A||B|\cos\theta=x_Ax_B+y_Ay_B+z_Az_B,$$
then $$1\cdot1\cdot\cos\theta=\cos\alpha\cos\alpha'+\cos\beta\cos\beta'+\cos\gamma\cos\gamma'.$$

 

[cpsinkule]

the law of cosines and the dot product formula are two equivalent statements. you can derive one from the other, so i don't think it matters which you use

 

[tommyxu3]

the law of cosines and the dot product formula are two equivalent statements. you can derive one from the other, so i don't think it matters which you use

Why do you think they are equivalent?
Moreover, here using cosine law may be harder to get the anticipated result.

 

[cpsinkule]

Why do you think they are equivalent?
Moreover, here using cosine law may be harder to get the anticipated result.

if you take the dot product formula as being true, then you can derive the law of cosines

if you take the law of cosines to be true, you can derive the dot product formula

 

[Karol]

The book asked to prove
$$\cos\theta=\cos\alpha\cos\alpha'+\cos\beta\cos\beta'+\cos\gamma\cos\gamma'$$
Before they taught the dot product, and they said i have to prove it with trigonometric considerations.
I made a mistake in writing in the OP about the dot product since when i was asked to prove it i wasn't expected to know about the dot product.

 

[tommyxu3]

Yes, then you could use cosine law.
For $A=(\cos\alpha,\cos\beta,\cos\gamma),B=(\cos\alpha',\cos\beta',\cos\gamma'),$ the triangle they make may have the third side, which we can present it as a vector $C$ that $C=A-B=(\cos\alpha-\cos\alpha',\cos\beta-\cos\beta',\cos\gamma-\cos\gamma').$
Now use cosine law:
$$|C|^2=|A|^2+|B|^2-2|A||B|\cos\theta$$
$$\Rightarrow(\cos\alpha-\cos\alpha')^2+(\cos\beta-\cos\beta')^2+(\cos\gamma-\cos\gamma')^2=(\cos\alpha)^2+(\cos\beta)^2+(\cos\gamma)^2+(\cos\alpha')^2+(\cos\beta')^2+(\cos\gamma')^2-2\cdot 1\cdot 1\cdot \cos\theta$$
$$\Rightarrow\cos\theta=\cos\alpha\cos\alpha'+\cos\beta\cos\beta'+\cos\gamma\cos\gamma'$$
$Q.E.D.$

 

[Karol]

I thank you very much tommyxu3, i am not sure that that is what they meant by trigonometric considerations, especially not the presentation of C as the subtraction of 2 vectors but it's good and the best i had, it really satisfied me, tommyxu3, thanks