- #1
#neutrino
- 51
- 2
if
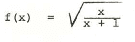 then to prove an inverse of this exists the following has been done to show that it is one to one
then to prove an inverse of this exists the following has been done to show that it is one to one
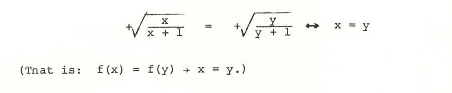
what is the basis of equating the 2 square roots ?
what is the basis of equating the 2 square roots ?