- #1
ChiralSuperfields
- 1,206
- 132
- Homework Statement
- Pls see the statement below
- Relevant Equations
- Binomial theorem
Why when proving trig identities,
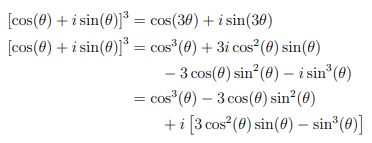
Do we assume that r = 1 from ## rcis\theta = r[\cos\theta + i\sin\theta]##? This makes me think that this is somehow it is related the unit circle.
Note: I am trying to prove the ##cos3\theta## identity and am curious why we assume that the modulus is 1.
Many thanks!
Do we assume that r = 1 from ## rcis\theta = r[\cos\theta + i\sin\theta]##? This makes me think that this is somehow it is related the unit circle.
Note: I am trying to prove the ##cos3\theta## identity and am curious why we assume that the modulus is 1.
Many thanks!