- #1
the_dialogue
- 79
- 0
Homework Statement
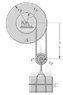
See attached image.
I'm wondering how one would express the velocity of C with respect to the angular velocity of the pulleys and the radii.
Homework Equations
v=w*r
The Attempt at a Solution
I've never quite done double pulleys such as these. Usually, If i had a single object attached, using one cable, to the edge of a pulley, its velocity would be 'v=wr' where 'r' is the radii of the pulley where the cable lies. But how about this case?
PS. This is not an assignment. It's merely a question I came across reading my book.
Attachments
Last edited: