- #1
EE4life
- 63
- 2
Hi all,
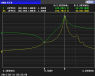
Given the impedance spectrum of a resonance circuit, I know that in order to calculate the Q factor we find the 3db bandwidth and then we use the following equation
Q = f_r/f_3dbbandwidth,
to find Q.
My question is how can I use, for example, the 1db bandwidth to calculate the Q factor. There should be some multiplication factor in there somewhere for this case.
Thank you
Given the impedance spectrum of a resonance circuit, I know that in order to calculate the Q factor we find the 3db bandwidth and then we use the following equation
Q = f_r/f_3dbbandwidth,
to find Q.
My question is how can I use, for example, the 1db bandwidth to calculate the Q factor. There should be some multiplication factor in there somewhere for this case.
Thank you
Last edited: