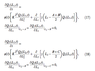- #1
nigels
- 36
- 0
Hi group,
I'm currently trying to understand a physicists written paper on ecological models. In there, they used the term "quadratic potential" when comparing spatial diffusion with a spring system (see attachment 1). After searching online for this term, I found nothing directly relevant to the material at hand. Can someone tell me what it means intuitively, whether it's represented by a canonical equation, and if so, whether the derivation of that gives the form seen in the paper (attachment 2)? Thanks!
For the original equations the variables in attachment 2 refers to, see attachment (3).
I'm currently trying to understand a physicists written paper on ecological models. In there, they used the term "quadratic potential" when comparing spatial diffusion with a spring system (see attachment 1). After searching online for this term, I found nothing directly relevant to the material at hand. Can someone tell me what it means intuitively, whether it's represented by a canonical equation, and if so, whether the derivation of that gives the form seen in the paper (attachment 2)? Thanks!
For the original equations the variables in attachment 2 refers to, see attachment (3).