Quantum Mechanics: Tunneling, Help

[nhk150709]

I have no idea how to solve these problems.
Picture is attached.

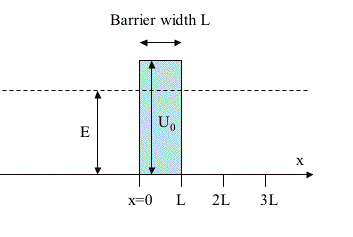
An electron with energy E is incident on a barrier of height U0 and total width L. It enters the barrier at x = 0, from the left.

1) For an electron with energy E = 6 eV and a barrier of height U0 = 12 eV, at what penetration depth into the barrier will the probability density fall to 1/4 of its value at the surface x = 0 ? Assume the barrier width L is sufficiently large that the in-barrier wavefunction is well approximated by a single exponential, i.e., negligible reflections from the x = L interface. [For an electron, mec2 = 0.511 MeV.]

0.055 nm
0.110 nm
0.282 nm
0.159 nm
0.319 nm
2) What is the probability density for this electron at the depth 3 times as large as the answer to the previous question, compared to its value at x = 0 ? Assume that the electron is still inside the barrier at this depth.

1/12
(1/4) 2
(1/4) 35) For the same barrier width L, if the height of the barrier and the energy of the electron are both reduced by a factor of 4, U1 = 0.25 U0 and E1 = 0.25 E, what is the transmission coefficient T1?

T1 = 10-8/4= 0.25 x 10-8
T1 = 10-8
T1 = 4 x 10-8
T1 = 2 x 10-4
The problem does not provide enough information to answer this question.

 

[Maxim Zh]

The general approach is to solve Schrodinger equation for 3 regions:
x < 0;
0 < x < L;
x > L;
and then build the solution for whole space, using wave function and it's derivative continuity. This allows to answer 5).

For large L this procedure gives:

$$\left|\frac{\psi(x)}{\psi(0)}\right|^2 = \exp(-2\alpha x).$$

That's enough to answer the question 2). For 1) you need to know $$\alpha$$.

The procedure described above is not convenient for complex barriers. The transfer-matrix method is more effective and gives the transmission coefficient explicitly.