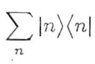Quantum Mechanics with DIRAC NOTATION

[JamesJames]

These are three quantum mechanics questions that I am having trouble with.

a) Calculate <alpha/beta> by converting to standary notation.
b) Prove that A is the identity operator where the sum is overa complete set of states. A is given in the attachment labelled by b
c) IF the state C is properly normalized, demonstrate the condition that an must satisfy. What is the interpretation of |an^2|? C is given in the attachment labelled by b

For a), I think it shoud be Psisubalpha(x) but the professor says I need some kind of integral?

For b), what I am trying to show? If someone could tell me that, it might help me a lot with this.

For c) I am genuinely lost . I think that |an^2| means the probability of being in the state n...that; s all I can come up with.

Any help would be greate guys. I need it desparately

James

 

[Fredrik]

a) I guess what they call "standard notation" is to express everything in terms of wavefunctions instead of state vectors in Dirac notation. Do you know the definition of the scalar product of two wavefunctions?

The wavefunction that corresponds to

|\alpha\rangle

is

\psi_\alpha(x)=\langle x|\alpha\rangle

Perhaps you can also get a clue from problem b. (Think x instead of n, and integral instead of sum).

b) You're trying to show that

A|\alpha\rangle=|\alpha\rangle

for any |\alpha\rangle.

c) Close, but not quite right. The physical system is in state |\alpha\rangle, so the probability that that the system is in state |n\rangle is zero. However, the probability that a measurement (of what?) will yield a certain result and leave the system in state |n\rangle...

 

[JamesJames]

ok so then for part a) would it just be <alpha/beta> = integral(Qdx) where Q = Psisubalphaconjugate(x)*Psisubbeta(x)

For c) the probability that a measurement OF <alpha|alpha> will yield a certain result and leave the system in state |n> is 1. This is what I think but I am not sure what to make of this.

 

[JamesJames]

Also, can you explain a bit more about part b)

 

[Fredrik]

a) That's the correct answer. The correct way of of getting it from \langle\alpha|\beta\rangle is to expand |\beta\rangle in position eigenkets.

c) No, \langle\alpha|\alpha\rangle is not a measureable quantity (and is also always =1). You can only measure Hermitean (i.e. self-adjoint) operators. What operator have you measured if the system is left in state |n\rangle?

It might be a good idea to learn some LaTeX.

 

[Fredrik]

b) I recommend that you prove it by showing that

\langle\alpha|A|\alpha\rangle=1=\langle\alpha|\alpha\rangle

 

[JamesJames]

What operator have you measured if the system is left in state |n> ?

I would say the operator is x although am not sure how I would determine this?

 

[Fredrik]

The answer depends on how the |n> states are defined of course, and I don't know how they're defined in this particular problem.

What you need to know is this:

When an observable (i.e. Hermitean operator) is measured, the result is always an eigenvalue of that observable, and the system is always left in an eigenstate of that operator. Remember the definition of eigenvalues and eigenvectors?

A|a\rangle=a|a\rangle

Here |a> is an eigenvector of A and a the eigenvalue that corresponds to the eigenvector |a>. If you measure A, and get the result a, the system will be left in the state described by the eigenvector |a>.

Now, the |a> states are a basis for the Hilbert space, so any state can be expressed as a linear combination of them:

|\alpha\rangle=\sum_a c_a |a\rangle

If the system is in state |\alpha\rangle when the measurement is made, what is the probability that the result will be a?

 

[JamesJames]

I would say it is csuba.

 

[Fredrik]

Is c_a a real number between 0 and 1? If it isn't, it can't be a probability, right?

This is actually very basic stuff that must be covered in your QM textbook, in the first or second chapter.

The probability amplitude is the projection of the state vector in the "direction" of the eigenstate:

\langle a|\alpha\rangle=c_a

so the probability is

|\langle a|\alpha\rangle|^2=|c_a|^2

 

[JamesJames]

Oh so the condition that the an must satisfy is then just

sum(|an|^2, n = 1..infinity) = 1

right? This will ensure normalization. We were told that psi*psi is the probability density. Is the probability density what you are calling the probability amplitude?

 

[Fredrik]

Oh so the condition that the an must satisfy is then just

sum(|an|^2, n = 1..infinity) = 1

right? This will ensure normalization.

Correct.

We were told that psi*psi is the probability density. Is the probability density what you are calling the probability amplitude?

No. A probability density is a real number. If you multiply it by a volume, you get a probability. A probability amplitude is a complex number. When you calculate the square of its absolute value, you get a probability.