How Does the Quantum Monty Hall Problem Challenge Classical Probability?

[Nick666]

So yesterday I saw this video with the monty hall problem, where you have 2 goats and a car each behind a door, each door having 1/3 chance of having the car, we choose door A to win the car, door B with the goat is revealed, so now doors A and C don't have 1/2 chance of having the car as intuition would say, but 1/3 for door A and 2/3 for door C .

So I started thinking if there is some equivalent quantum experiment of the monty hall problem.

And apparently there is: http://arxiv.org/pdf/quant-ph/0202120v1.pdf

and http://www.scielo.br/scielo.php?script=sci_arttext&pid=S0001-37652006000300003

I haven't tried to understand the first paper, but the second one says "Starting from the an initial "equiprobable" state (with the natural choice M1,2 =

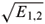for the measurement operators) leads to identical conclusions, concerning the MHP puzzle, as in the classical probabilistic reasoning. It is remarkable that the argument leading to these conclusions seems to be more straightforward in the quantum than in the classical setting. It is perhaps not too farfetched to assert that the correct answer to the MHP puzzle is "embodied" in the very formalism of quantum mechanic's measurement theory. "

But wouldn't that mean that in the quantum world just like in the classical world, probabilities are just a mathematical tool that only affects our state of knowledge and have no bearing on what is actually going on ?

 

[bhobba]

But wouldn't that mean that in the quantum world just like in the classical world, probabilities are just a mathematical tool that only affects our state of knowledge and have no bearing on what is actually going on ?

Its different.

Bells Theorem shows quantum correlations are different to classical ones.

Thanks
Bill

 

[Ken G]

Another important thing to recognize about the MHP that is often insufficiently stressed is that the correct answer to the probability depends on "Monty's rules," i.e., what assumptions we are making about Monty's behavior. The usual assumption is that Monty is a trickster, who, just to stir the pot, will intentionally show you a goat after you have picked your door (noting that there will always be a goat left to show). So this requires that Monty knows what is behind the doors, and you are in effect borrowing from Monty's knowledge if you decide to switch doors. If Monty has no knowledge, and just showed you a door at random, then it is correct to increase your probability to 1/2 when you renormalize the probabilities to make them add up to 1, but if Monty knew he was showing you a goat, that does not alter your original 1/3 chance, there is no need to renormalize because nothing of importance to your original chances of winning has changed. So the MHP puzzle is not actually a puzzle that relates to the surprising aspects of probability, it is a puzzle that relates to the surprising connections between information and probability, and what constitutes information that would cause you to reassess your probability-- and what doesn't. No light is shined on that aspect of the problem in these quantized analyses, for they simply assume the standard Monty's rules, where to me the whole interest of this puzzle is the connection between Monty's information and the player's. If someone wants to convince me that this rather trivial puzzle can be understood better in the language of quantum probability, then they need to convince me I can better understand the general state of that information connection.

Also, in regard to the second article, I find another missing part of their argument that I feel is important. They correctly conclude that if they start with a superposition state of the car being in any of the boxes, and further stipulate that the car is equally likely to be in any box, then they recover the classical result that the player (given Monty's rules) can get a 2/3 chance of winning by switching doors. They regard this as a success of the quantized theory, even going so far as to suggest that the classical answer might in some sense emerge from the quantum situation. But this overlooks a rather important wrinkle-- they imply that there are initial superposition states that do not correspond to equally likely locations for the car for which their formalism would not give the classical answer. This implication comes from their restricting their formalism to that case-- if it is more generally true, then their argument is certainly incomplete. But if it is not generally true, then their argument is wrong, because it is clear in the classical situation that there is no requirement whatsoever on the probability distribution on where the car is placed. So if there is a requirement on the quantum superposition, then it is that requirement, and not what they showed with their overall formalism, that asserts the connection with the classical answer. So we are left with this important question-- if there are superpositions that do not give the classical answer, then the only way we could argue that the classical result "emerges" from the quantum result is by showing how it emerges from the particular requirements that initial superposition must exhibit in order to produce the classical answer. Presumably it has to do with the absence of coherences in the initial density matrix, but if so, that gives the whole argument the flavor of having been reversed: they claim they are showing the classical result using quantum language, when in fact they have embedded the classical result in the quantum language right from the get go. If this is true, then there must be something singular in the "equal probability" initial state that renders it "more classical" than the other possibilities (though I'm sure "definitely behind one door" is going to be an equally classical type of superposition).

If instead their argument goes through for all initial superpositions, then they should show that too. But even still, I'm not convinced I have a simpler way to think of the puzzle in that language, I want to see how a range of "Monty's rules" plays out in the quantum language, such that I can analyze them more straightforwardly in that regime, and get insight into how the player can gain information from Monte's actions. If that is possible, we might see theoretical physicists using it to play poker!

 

[mathman]

If Monty has no knowledge, and just showed you a door at random, then it is correct to increase your probability to 1/2 when you renormalize the probabilities to make them add up to 1,

True. If he picks a door at random there is a 1/3 probability that he will open the door to the car.

 

[Ken G]

Right, so what the contestant is doing by changing is simply piggy-backing off the help Monty is giving them if he knows where the goats are. This is especially simple to see if there are 100 doors, 1 car and 99 goats, and Monty reveals 98 goats. Then there's your door, and door #42, as the only ones left. Are you going to stick with your door, when door #42 practically has bells and whistles attached to it? So there's nothing interesting we need to borrow from the quantum domain to understand this very classical problem. It's only interesting if the quantum domain gives us some kind of new and more powerful language to talk about the process whereby we are extracting information from Monty's actions, perhaps in situations where his strategy is more complicated and there might be some value to imagine that the goats are in some kind of superposition. That would be an interesting application to a classical area of a quantum notion, but the way they set it up, with just the simple Monty's rules, and just the equal-probability superposition, it's not clear to me that there's much to gain from this analysis.

 

[Demystifier]

But wouldn't that mean that in the quantum world just like in the classical world, probabilities are just a mathematical tool that only affects our state of knowledge and have no bearing on what is actually going on ?

In QM you can move the "goat" by opening the "door".